12th Grade > Mathematics
DEFINITE INTEGRATION MCQs
Total Questions : 30
| Page 2 of 3 pages
Answer: Option B. -> π2
:
B
∫π2−π2sin2xdx=2∫π20sin2xdx=2r(32)r(12)2r(2+22)=π2
:
B
∫π2−π2sin2xdx=2∫π20sin2xdx=2r(32)r(12)2r(2+22)=π2
Answer: Option B. -> 1
:
B
We can see that the given integral is an improper integral as one of its limits is not finite.
In such cases where we have to deal with infinity as the limits of definite integral, we’ll change the limit which is not finite to a variable and then put the limits.
∞∫0e−xdx=lima→∞a∫0e−xdx
=lima→∞(−e−x)a0
=lima→∞(−e−a−(−e0))
=0−(−1)
=1
:
B
We can see that the given integral is an improper integral as one of its limits is not finite.
In such cases where we have to deal with infinity as the limits of definite integral, we’ll change the limit which is not finite to a variable and then put the limits.
∞∫0e−xdx=lima→∞a∫0e−xdx
=lima→∞(−e−x)a0
=lima→∞(−e−a−(−e0))
=0−(−1)
=1
Answer: Option A. -> π log 2
:
A
∫π20log(tanx+cotx)dx=∫π20log[2sin2x]dx
=∫π20(log2−logsin2x)dx=log2(π2)+(π2)log2=πlog2
:
A
∫π20log(tanx+cotx)dx=∫π20log[2sin2x]dx
=∫π20(log2−logsin2x)dx=log2(π2)+(π2)log2=πlog2
Answer: Option A. -> 20
:
A
∴∫10π0|sinx|dx=10∫π0|sinx|dx
∴|sinx|is positive in I & II quadrant and has period π
=10∫π0sinxdx=10[−cosx]x0=20
:
A
∴∫10π0|sinx|dx=10∫π0|sinx|dx
∴|sinx|is positive in I & II quadrant and has period π
=10∫π0sinxdx=10[−cosx]x0=20
Answer: Option B. -> 21
:
B
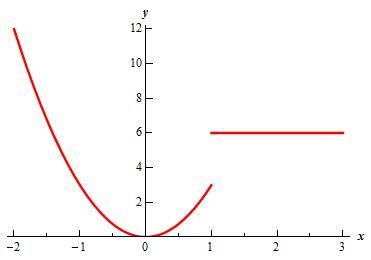
Here, we can see that the integrand f(x) in not continuous in the interval (-2, 3) as it has a discontinuity at x = 1. So we can’t just integrate f(x) and put limits.We’ll have to break this integral into integrals which have limits such that integrands is continuous in those limits.
∫3−2f(x)dx=∫1−23x2dx+∫316dx
Now we can integrate these integrands and put limits.
∫1−23x2dx+∫316dx=(x3)|1−2+(6x)|31=1−(−8)+18−6
= 21
:
B
Here, we can see that the integrand f(x) in not continuous in the interval (-2, 3) as it has a discontinuity at x = 1. So we can’t just integrate f(x) and put limits.We’ll have to break this integral into integrals which have limits such that integrands is continuous in those limits.
∫3−2f(x)dx=∫1−23x2dx+∫316dx
Now we can integrate these integrands and put limits.
∫1−23x2dx+∫316dx=(x3)|1−2+(6x)|31=1−(−8)+18−6
= 21
Answer: Option B. -> 1100
:
B
limπ→∞199+299+399+⋯⋯n99n100=limπ→∞∑nr=1(r99n100)
=limπ→∞1n∑nr=1(rn)99=∫10x99dx=[x100100]10=1100
:
B
limπ→∞199+299+399+⋯⋯n99n100=limπ→∞∑nr=1(r99n100)
=limπ→∞1n∑nr=1(rn)99=∫10x99dx=[x100100]10=1100
Answer: Option A. -> [0,117]
:
A
f(x)=xx3+16⇒f′(x)=16−2x3(x3+16)2∴f′(x)=0⇒x=2Alsof′′(2)<0⇒ The function f(x)=xx3+16 is an increasing function in [0,1], so Min f(x) = f(0) = 0 and Max f(x) = f(1) = 117
Therefore by the property m(b−a)≤∫baf(x)dx≤M(b−a)
(where m and M are the smallest and greatest values of function)
⇒0≤∫10xx3+16dx≤117
:
A
f(x)=xx3+16⇒f′(x)=16−2x3(x3+16)2∴f′(x)=0⇒x=2Alsof′′(2)<0⇒ The function f(x)=xx3+16 is an increasing function in [0,1], so Min f(x) = f(0) = 0 and Max f(x) = f(1) = 117
Therefore by the property m(b−a)≤∫baf(x)dx≤M(b−a)
(where m and M are the smallest and greatest values of function)
⇒0≤∫10xx3+16dx≤117
Answer: Option A. -> log 2
:
A
put 1+ sin x =t
Then∫π20cosx1+sinxdx=[log|1+sinx|]π20=log2
:
A
put 1+ sin x =t
Then∫π20cosx1+sinxdx=[log|1+sinx|]π20=log2
Answer: Option A. -> 12
:
A
∫x0dt=x+∫1xtf(t)dt⇒∫1xtf(t)dt=x−∫x1tf(t)dt
Differentiating w.r.t x, we get f(x)=1+{0−xf(x)}
⇒f(x)=1−xf(x)⇒(1+x)f(x)=1⇒f(x)=11+x
∴f(1)=11+1=12
:
A
∫x0dt=x+∫1xtf(t)dt⇒∫1xtf(t)dt=x−∫x1tf(t)dt
Differentiating w.r.t x, we get f(x)=1+{0−xf(x)}
⇒f(x)=1−xf(x)⇒(1+x)f(x)=1⇒f(x)=11+x
∴f(1)=11+1=12
Answer: Option A. -> a1,a2,a3.....are in A.P.
:
A
In=(xn+1n+1tan−1x)10−∫10xn+1n+1.11+x2dx(n+1)In=π4−∫10xn+11+x2dx(n+3)In+2=π4−∫10xn+31+x2dx∴(n+1)In+(n+3)In+2=π2−1n+2∴an=(n+3)⇒a1,a2,a3.....are in A.P.
bn=(n+1)⇒b1,b2..... are in A.P.
cn=π2−1n+2 not in any progression.
:
A
In=(xn+1n+1tan−1x)10−∫10xn+1n+1.11+x2dx(n+1)In=π4−∫10xn+11+x2dx(n+3)In+2=π4−∫10xn+31+x2dx∴(n+1)In+(n+3)In+2=π2−1n+2∴an=(n+3)⇒a1,a2,a3.....are in A.P.
bn=(n+1)⇒b1,b2..... are in A.P.
cn=π2−1n+2 not in any progression.
Latest Videos
Latest Test Papers
Login With Google
Old way of Login
Login With Email