Question
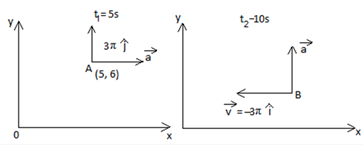
A particle moves along a circular path over a horizontal xy coordinate system, at constant speed. At time t1 = 5.00 s, it is at point (5.00 m, 6.00 m) with velocity (3π m/s)^j and acceleration in the positive x direction. At time t2 = 10.0 s, it has velocity (-3π m/s)^i and acceleration in the positive y direction. What are the (a) x and (b) y coordinates of the center of the circular path if t2 - t1 is less than one period?
A particle moves along a circular path over a horizontal xy coordinate system, at constant speed. At time t1 = 5.00 s, it is at point (5.00 m, 6.00 m) with velocity (3π m/s)^j and acceleration in the positive x direction. At time t2 = 10.0 s, it has velocity (-3π m/s)^i and acceleration in the positive y direction. What are the (a) x and (b) y coordinates of the center of the circular path if t2 - t1 is less than one period?
Answer: Option A
:
A
We know the body is undergoing uniform circular motion,
∴ only possible path is
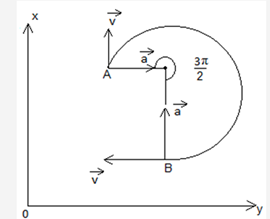
As acceleration should always be directed toward the centre
To calculate the position of the centre, we need the radius, to calculate radius,v=ωr we can use the relation,as we can calculate ω
Δθ=3π2,Δt=5s
=3π2×5=3π10S−1
usingv=ωr
r=vω
|→v|=3πm/sgiven
∴r=3π3π10=30π3π=10m
∴ifr=10m, coordinates of the centre (15 m,6m)
Was this answer helpful ?
:
A
We know the body is undergoing uniform circular motion,

∴ only possible path is

As acceleration should always be directed toward the centre
To calculate the position of the centre, we need the radius, to calculate radius,v=ωr we can use the relation,as we can calculate ω
Δθ=3π2,Δt=5s
=3π2×5=3π10S−1
usingv=ωr
r=vω
|→v|=3πm/sgiven
∴r=3π3π10=30π3π=10m
∴ifr=10m, coordinates of the centre (15 m,6m)
Was this answer helpful ?


















Submit Solution