12th Grade > Physics
KINEMATICS MCQs
Circular Kinematics
Total Questions : 41
| Page 1 of 5 pages
Answer: Option C. -> constant kinetic energy
:
C
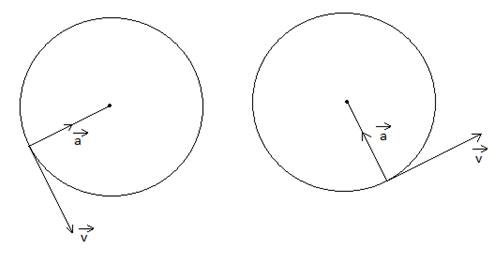
We can see that direction of velocity and acceleration changes continuously
∴ Both are not constant.
Momentum is m.⃗v which depends on velocity and changes with velocity.
The only quantity that is constant is speed and kinetic energy is 12m|⃗v|2 where|⃗v| is the speed.
∴ Answer is kinetic energy.
:
C

We can see that direction of velocity and acceleration changes continuously
∴ Both are not constant.
Momentum is m.⃗v which depends on velocity and changes with velocity.
The only quantity that is constant is speed and kinetic energy is 12m|⃗v|2 where|⃗v| is the speed.
∴ Answer is kinetic energy.
Answer: Option A. -> 40π2
:
A
Att1=2s,→a=(5√3ms2)^i+5^j
Att2=5s,→a=(5ms2)^i−(5√3ms2)^i+^j
Given the body is moving in anti-clockwise direction
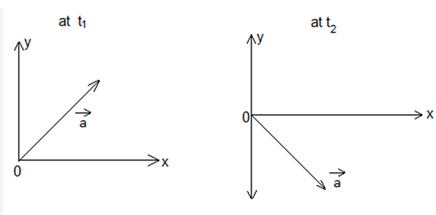
Since,the speed is constant, net acceleration will always be directed toward the centre and since it is
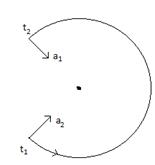
This will be the only path possible using this, we can calculate ω as we can find the change in angle
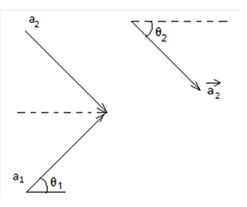
tanθ1=15√3=13
tanθ2=3√35=√3
∴θ1=30∘
⇒θ2=60∘
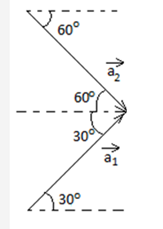
∴ We can see that angle between the vectors is 90∘ which means particle would have covered an angle of 360−90=270∘=3π/2radin3s
∴ω=ΔθΔt=3π23=π2rad/s
a=ω2r
r=aω2=√(5√3)2+52(π2)2=√100π24
=4×10π2=40π2
:
A
Att1=2s,→a=(5√3ms2)^i+5^j
Att2=5s,→a=(5ms2)^i−(5√3ms2)^i+^j
Given the body is moving in anti-clockwise direction

Since,the speed is constant, net acceleration will always be directed toward the centre and since it is

This will be the only path possible using this, we can calculate ω as we can find the change in angle

tanθ1=15√3=13
tanθ2=3√35=√3
∴θ1=30∘
⇒θ2=60∘

∴ We can see that angle between the vectors is 90∘ which means particle would have covered an angle of 360−90=270∘=3π/2radin3s
∴ω=ΔθΔt=3π23=π2rad/s
a=ω2r
r=aω2=√(5√3)2+52(π2)2=√100π24
=4×10π2=40π2
Answer: Option D. -> 1
:
D
ω1=△θ△t
If time taken to complete a revolution is t.
Then ω1=2πt,ω2=2πt
⇒t=2πω1=2πω2
⇒ we get ω1=ω2orω1ω2=1
:
D
ω1=△θ△t
If time taken to complete a revolution is t.
Then ω1=2πt,ω2=2πt
⇒t=2πω1=2πω2
⇒ we get ω1=ω2orω1ω2=1
Answer: Option B. -> Q
:
B
If a particle goes in a circle with constant ω then it has a centripetal acceleration given by ω2R since ω is constant for both particles. So the acceleration depends on R
∵RQ>RP
⇒ω2RQ>ω2RP
So particle q will have higher centripetal acceleration.
:
B
If a particle goes in a circle with constant ω then it has a centripetal acceleration given by ω2R since ω is constant for both particles. So the acceleration depends on R
∵RQ>RP
⇒ω2RQ>ω2RP
So particle q will have higher centripetal acceleration.
Answer: Option B. -> R1
:
B
Reaction on inner wheel R1=12M[g−v2hra]
Reaction on outer wheel R2=12M[g+v2hra]
where, r = radius of circular path, 2a = distance between two wheels and h = height of centre of gravity of car.
:
B
Reaction on inner wheel R1=12M[g−v2hra]
Reaction on outer wheel R2=12M[g+v2hra]
where, r = radius of circular path, 2a = distance between two wheels and h = height of centre of gravity of car.
Answer: Option C. -> Tangentially outward
:
C
Stone flies in the direction of instantaneous velocity due to inertia
:
C
Stone flies in the direction of instantaneous velocity due to inertia
Question 7.
A purse at radius 2.00 m and a wallet at radius 3.00 m travel in uniform circular motion on the floor of a merry-go-round as the ride turns. They are on the same radial line. At one instant, the acceleration of the purse is (2.00 m/ s2)^i + (4.00 m/ s2)^j . At that instant and in unit-vector notation, what is the acceleration of the wallet? IIT JEE- 2001
A purse at radius 2.00 m and a wallet at radius 3.00 m travel in uniform circular motion on the floor of a merry-go-round as the ride turns. They are on the same radial line. At one instant, the acceleration of the purse is (2.00 m/ s2)^i + (4.00 m/ s2)^j . At that instant and in unit-vector notation, what is the acceleration of the wallet? IIT JEE- 2001
Answer: Option C. -> 3 ^i + 6 ^j
:
C
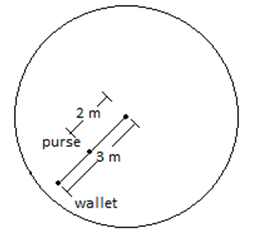
dθdt is constant.
In other words in uniform circular motion the angular velocity remains constant body doesn't have any tangential acceleration but normal acceleartion.
aN=v2Rorω2R
ForpurseaN=√(2)2+(4)2=√20;R=2
⇒√20=ω22
⇒ω2=√5
ForwalletaN=ω2R
Hence ωis same
But~R=3
⇒aN=√5×3
aN=3√5
So the above answer matches with the magnitude of third option in the given answers.
:
C

dθdt is constant.
In other words in uniform circular motion the angular velocity remains constant body doesn't have any tangential acceleration but normal acceleartion.
aN=v2Rorω2R
ForpurseaN=√(2)2+(4)2=√20;R=2
⇒√20=ω22
⇒ω2=√5
ForwalletaN=ω2R
Hence ωis same
But~R=3
⇒aN=√5×3
aN=3√5
So the above answer matches with the magnitude of third option in the given answers.
Answer: Option B. -> √{v4r2+a2}
:
B
aresultant=√a2radial+a2tangential=√v4r2+a2
:
B
aresultant=√a2radial+a2tangential=√v4r2+a2
Answer: Option B. -> 20 π m / minute
:
B
The linear speed is,
v = r ω ;ω = θt
Substituting, we get,
v=20 π m / minute
:
B
The linear speed is,
v = r ω ;ω = θt
Substituting, we get,
v=20 π m / minute
Question 10.
A particle moves along a circular path over a horizontal xy coordinate system, at constant speed. At time t1 = 5.00 s, it is at point (5.00 m, 6.00 m) with velocity (3π m/s)^j and acceleration in the positive x direction. At time t2 = 10.0 s, it has velocity (-3π m/s)^i and acceleration in the positive y direction. What are the (a) x and (b) y coordinates of the center of the circular path if t2 - t1 is less than one period?
A particle moves along a circular path over a horizontal xy coordinate system, at constant speed. At time t1 = 5.00 s, it is at point (5.00 m, 6.00 m) with velocity (3π m/s)^j and acceleration in the positive x direction. At time t2 = 10.0 s, it has velocity (-3π m/s)^i and acceleration in the positive y direction. What are the (a) x and (b) y coordinates of the center of the circular path if t2 - t1 is less than one period?
Answer: Option A. -> (15 m, 6 m)
:
A
We know the body is undergoing uniform circular motion,
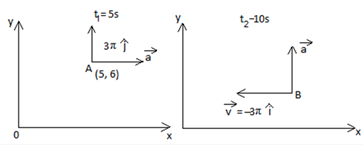
∴ only possible path is
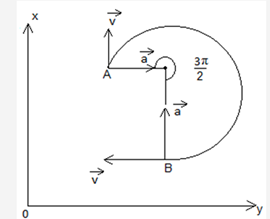
As acceleration should always be directed toward the centre
To calculate the position of the centre, we need the radius, to calculate radius,v=ωr we can use the relation,as we can calculate ω
Δθ=3π2,Δt=5s
=3π2×5=3π10S−1
usingv=ωr
r=vω
|→v|=3πm/sgiven
∴r=3π3π10=30π3π=10m
∴ifr=10m, coordinates of the centre (15 m,6m)
:
A
We know the body is undergoing uniform circular motion,

∴ only possible path is

As acceleration should always be directed toward the centre
To calculate the position of the centre, we need the radius, to calculate radius,v=ωr we can use the relation,as we can calculate ω
Δθ=3π2,Δt=5s
=3π2×5=3π10S−1
usingv=ωr
r=vω
|→v|=3πm/sgiven
∴r=3π3π10=30π3π=10m
∴ifr=10m, coordinates of the centre (15 m,6m)
















