Kinematics(12th Grade > Physics ) Questions and answers for exam Preparation

12th Grade > Physics

KINEMATICS MCQs

Circular Kinematics

Total Questions : 41 | Page 3 of 5 pages

Question 21. A balloon starts rising from the surface of the Earth. The ascension rate is constant and equal to v_o. Due to the wind the balloon gathers the horizontal velocity component v_x=ay, where a is a constant and y is the height of ascent. Find the total, tangential, and normal accelerations of the balloon.

ar=av0;at=av0√1+(ayv0)2;aN=av0
ar=av0;at=av0;aN=0
ar=av0;at=a2y√1+a2y2v20;aN=av0 ⎷(1+a2y2v20)
ar=a2y√1+a2y2v20;at=av0;aN=av0

Discuss Question

Answer: Option C. -> ar=av0;at=a2y√1+a2y2v20;aN=av0 ⎷(1+a2y2v20)
:
C
The path of the balloon will look something like this

A Balloon Starts Rising From The Surface Of The Earth. The A...

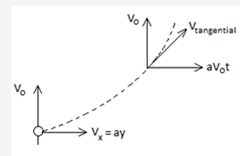
After t sec ballon would have gone a height of

v_{0} t

then at that very instance the balloon's

v_{x}

will be

v_{x} = a v_{0} t \Rightarrow a_{x} = a v_{0}

V_{y} = v_{0}

a_{y} = 0

a_{r} = t o t a l a c c e l e r a t i o n = a v_{0} . . . . . . . (1)

v_{t a n g e n t i c a l}

is actually the resultant velocity

\Rightarrow v_{t} = \sqrt{v^{2} 0 + (a v_{0} t)^{2}}

\Rightarrow v_{t} = v_{0} \sqrt{1 + a^{2} t^{2}}

a_{t} = \frac{d v_{t}}{d t} = \frac{v_{0} a^{2} t}{\sqrt{1 + a^{2} t^{2}}} \Rightarrow \frac{a^{2} y}{\sqrt{1 + {(\frac{a y}{v_{0}})}^{2}}}

Now we know

a_{t}^{2} + a_{N}^{2} = a_{r}^{2}

\Rightarrow \frac{v_{0}^{2} a^{4} t^{2}}{(1 + a^{2} t^{2})} + a_{N}^{2} = a^{2} v_{0}^{2}

a_{N} = \sqrt{v_{0}^{2} a^{4} t^{2} - \frac{v_{0}^{2} a^{4} t^{2}}{(1 + a^{2} t^{2})}}

a_{N} = a v_{0} \sqrt{\frac{1 + a^{2} t^{2} - a^{2} t^{2}}{(1 + a^{2} t^{2})}}

a_{N} = \frac{a v_{0}}{\sqrt{1 + a^{2} t^{2}}}

\Rightarrow \frac{a v_{0}}{\sqrt{1 + {(\frac{a y}{v_{0}})}^{2}}}

Question 22. A hollow vertical cylinder of radius R and height h has smooth internal surface. A small particle is placed in contact with the inner side of the upper rim at a point P. It is given a horizontal speed v_o tangential to rim. It leaves the lower rim at point Q, vertically below P. The number of revolutions made by the particle will

h2πR
v0√2gh
2πRh
v02πR(√2hg)

Discuss Question

Answer: Option D. -> v02πR(√2hg)
:
D
since the body has no initial velocity in the vertical direction.

A Hollow Vertical Cylinder Of Radius R And Height H Has Smoo...

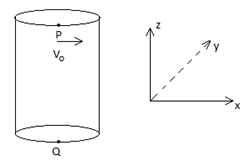
a_{z}

=-g, vertical displacement z=-h.

∴ z = a t + \frac{1}{2} a t^{2}

\Rightarrow - h = 0 + \frac{1}{2} (- g) t^{2}

\Rightarrow T = \sqrt{\frac{2 h}{g}}

time taken to reach the bottom
let,t be the time taken to complete one revolution.
Then

t = \frac{2 π R}{v_{0}}

∴

number of revolution=

\frac{T}{t} = \frac{\sqrt{\frac{2 h}{g}}}{\frac{2 π R}{v_{0}}} = \frac{v_{0}}{2 π R} \sqrt{\frac{2 h}{g}}

Question 23. Find the maximum velocity for skidding for a car moved on a circular track of radius 100 m. The coefficient of friction between the road and tyre is 0.2

0.14 m/s
140 m/s
1.4 km/s
14 m/s

Discuss Question

Answer: Option D. -> 14 m/s
:
D

V_{m a x} = \sqrt{μ r g} = \sqrt{0.2 \times 100 \times 9.8} = 14 m / s

Question 24. A point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of 'P' is such that it sweeps out a length