Question
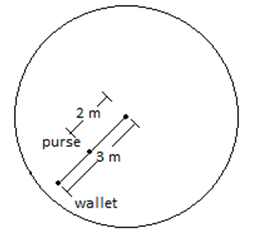
A purse at radius 2.00 m and a wallet at radius 3.00 m travel in uniform circular motion on the floor of a merry-go-round as the ride turns. They are on the same radial line. At one instant, the acceleration of the purse is (2.00 m/ s2)^i + (4.00 m/ s2)^j . At that instant and in unit-vector notation, what is the acceleration of the wallet? IIT JEE- 2001
A purse at radius 2.00 m and a wallet at radius 3.00 m travel in uniform circular motion on the floor of a merry-go-round as the ride turns. They are on the same radial line. At one instant, the acceleration of the purse is (2.00 m/ s2)^i + (4.00 m/ s2)^j . At that instant and in unit-vector notation, what is the acceleration of the wallet? IIT JEE- 2001
Answer: Option C
:
C
dθdt is constant.
In other words in uniform circular motion the angular velocity remains constant body doesn't have any tangential acceleration but normal acceleartion.
aN=v2Rorω2R
ForpurseaN=√(2)2+(4)2=√20;R=2
⇒√20=ω22
⇒ω2=√5
ForwalletaN=ω2R
Hence ωis same
But~R=3
⇒aN=√5×3
aN=3√5
So the above answer matches with the magnitude of third option in the given answers.
Was this answer helpful ?
:
C
dθdt is constant.
In other words in uniform circular motion the angular velocity remains constant body doesn't have any tangential acceleration but normal acceleartion.
aN=v2Rorω2R
ForpurseaN=√(2)2+(4)2=√20;R=2
⇒√20=ω22
⇒ω2=√5
ForwalletaN=ω2R
Hence ωis same
But~R=3
⇒aN=√5×3
aN=3√5
So the above answer matches with the magnitude of third option in the given answers.
Was this answer helpful ?
More Questions on This Topic :
Latest Videos
Latest Test Papers
Submit Solution