Quantitative Aptitude
GEOMETRY MCQs
Coordinate Geometry, Coordinate Geometry (10th Grade), Three Dimensional Geometry (10th Grade)
Total Questions : 133
| Page 6 of 14 pages
Answer: Option B. -> perpendicular
Answer: Option A. -> (–5, –2)
:
A
If a point P(x,y) divides a line segment joining (x1,y1)and(x2,y2) in the ratiom:n, then the coordinates of P are given by:
x=mx2+nx1m+n,y=my2+ny1m+n
Let C(−1,2) dividethe line joining A(2,5) and B(x,y) in the ratio 3:4.
Then,
C(3x+87,3y+207) = C(-1, 2)
⇒3x+87=−13x+8=−7⇒x=−5⇒3y+207=23y+20=14⇒y=−2
Thus, thecoordinates of B are B(−5,−2).
:
A
If a point P(x,y) divides a line segment joining (x1,y1)and(x2,y2) in the ratiom:n, then the coordinates of P are given by:
x=mx2+nx1m+n,y=my2+ny1m+n
Let C(−1,2) dividethe line joining A(2,5) and B(x,y) in the ratio 3:4.
Then,
C(3x+87,3y+207) = C(-1, 2)
⇒3x+87=−13x+8=−7⇒x=−5⇒3y+207=23y+20=14⇒y=−2
Thus, thecoordinates of B are B(−5,−2).
Answer: Option D. -> equilateral
:
D
Let's name the points asA(a,a),B(−a,−a) and C(–√3a,√3a).
By distance formula, distance between points (x1,y1) and (x2,y2)
=√(x2−x1)2+(y2−y1)2
BC=√(−√3a+a)2+(√3a+a)2=√a2+(√3a)2−2×a×√3a+√3a)2+a2+2×a×√3aBC=√8a2=2√2aunitsSimilarlyAB=√(a+a)2+(a+a)2=√8a2=2√2aunitsAC=√(−√3a−a)2+(√3a−a)2=√8a2=2√2aunits
Weget,AB=BC=AC=2√2aunits∴△ABC is an equilateral triangle.
:
D
Let's name the points asA(a,a),B(−a,−a) and C(–√3a,√3a).
By distance formula, distance between points (x1,y1) and (x2,y2)
=√(x2−x1)2+(y2−y1)2
BC=√(−√3a+a)2+(√3a+a)2=√a2+(√3a)2−2×a×√3a+√3a)2+a2+2×a×√3aBC=√8a2=2√2aunitsSimilarlyAB=√(a+a)2+(a+a)2=√8a2=2√2aunitsAC=√(−√3a−a)2+(√3a−a)2=√8a2=2√2aunits
Weget,AB=BC=AC=2√2aunits∴△ABC is an equilateral triangle.
Answer: Option B. -> (2, – 2)
:
B
Midpoint of theline segment joining (x1,y1) and (x2,y2) is given by (x1+x22,y1+y22)
∴ Mid-point of the line-segment joining the points (– 5, 4) and (9, – 8) = (−5+92,4−82) = (2,-2)
:
B
Midpoint of theline segment joining (x1,y1) and (x2,y2) is given by (x1+x22,y1+y22)
∴ Mid-point of the line-segment joining the points (– 5, 4) and (9, – 8) = (−5+92,4−82) = (2,-2)
Answer: Option C. -> (– 4, 4)
:
C
If a point P(x,y) divides the line joining (x1,y1)and(x2,y2) in the ratio m:n
thenx = mx2+nx1m+n and y =my2+ny1m+n
∴x = mx2+nx1m+n = 2(−5)+1(−2)2+1 = -4
and y = my2+ny1m+n = 2(7)+1(−2)2+1 = 4
∴ the required point is (-4,4).
:
C
If a point P(x,y) divides the line joining (x1,y1)and(x2,y2) in the ratio m:n
thenx = mx2+nx1m+n and y =my2+ny1m+n
∴x = mx2+nx1m+n = 2(−5)+1(−2)2+1 = -4
and y = my2+ny1m+n = 2(7)+1(−2)2+1 = 4
∴ the required point is (-4,4).
Answer: Option A. -> [−1√35,5√35,3√35]
:
A
If l, m, n are the d.c.’s of the line which is perpendicular to the given lines, then
l – m + 2n = 0 and 2l + m –n = 0
∴l1−2=m4+1=n1+2⇒l−1=m5=n3.
so d.r's =(−1,5,3)
:
A
If l, m, n are the d.c.’s of the line which is perpendicular to the given lines, then
l – m + 2n = 0 and 2l + m –n = 0
∴l1−2=m4+1=n1+2⇒l−1=m5=n3.
so d.r's =(−1,5,3)
Answer: Option A. -> 2x -4y +3z-8 =0
:
A
l+2m+2n=0, 3l+3m+2n=0, l2+m2+n2=1, we get l, m, nfrom these equations and then putting the values in l(x-1)+m(y+3) +n(z+2)=0, we get the required result.
Trick: Checking conversely,
2(x)-4(y)+3(z)-8 =0,
So, it passes through given point.
1(2)+2(-4)+2(3) =0,
So, it is perpendicular to x+2y+2z=5.
3(2)+3(-4)+2(3)=0,
So, it is perpendicular to 3x+3y +2z=8.
:
A
l+2m+2n=0, 3l+3m+2n=0, l2+m2+n2=1, we get l, m, nfrom these equations and then putting the values in l(x-1)+m(y+3) +n(z+2)=0, we get the required result.
Trick: Checking conversely,
2(x)-4(y)+3(z)-8 =0,
So, it passes through given point.
1(2)+2(-4)+2(3) =0,
So, it is perpendicular to x+2y+2z=5.
3(2)+3(-4)+2(3)=0,
So, it is perpendicular to 3x+3y +2z=8.
Answer: Option B. -> l1+l22cosθ2,m1+m22cosθ2,n1+n22cosθ2
:
B
Let OA and OB be two lines with d.c’s l1,m1,n1 and l2,m2,n2,. Let OA = OB = 1. Then, the coordinates of A and B are (l1,m1,n1) and (l2,m2,n2), respectively. Let OC be the bisector of ∠AOB .Then, C is the mid point of AB and so its coordinates are (l1+l22,m1+m22,n1+n22).
∴ d.r's of OC are l1+l22,m1+m22,n1+n22
We have, OC=√(l1+l22)2+(m1+m22)2+(n1+n22)2=12√(l21+m21+n21)+(l22+m22+n22)+(l1l2+m1m2+n1n2)=12√2+2cosθ[Qcosθ=l1l2+m1m2+n1n2]=12√2(1+cosθ)=cos(θ2)
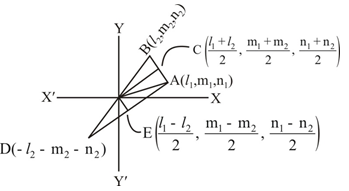
∴ d.c's of OC are
l1+l22(OC),m1+m22(OC),n1+n22(OC)
:
B
Let OA and OB be two lines with d.c’s l1,m1,n1 and l2,m2,n2,. Let OA = OB = 1. Then, the coordinates of A and B are (l1,m1,n1) and (l2,m2,n2), respectively. Let OC be the bisector of ∠AOB .Then, C is the mid point of AB and so its coordinates are (l1+l22,m1+m22,n1+n22).
∴ d.r's of OC are l1+l22,m1+m22,n1+n22
We have, OC=√(l1+l22)2+(m1+m22)2+(n1+n22)2=12√(l21+m21+n21)+(l22+m22+n22)+(l1l2+m1m2+n1n2)=12√2+2cosθ[Qcosθ=l1l2+m1m2+n1n2]=12√2(1+cosθ)=cos(θ2)

∴ d.c's of OC are
l1+l22(OC),m1+m22(OC),n1+n22(OC)
Answer: Option B. -> 92
:
B
Any point onx−12=y+13=z−14=λ is,
(2λ+1,3λ−1,4λ+1);λ∈R
Any point on x−31=y−k2=z1=μ is,
(μ+3,2μ+k,μ);μ∈R
the given lines intersect if and only if the system of equations(in λ and μ)
2λ+1=μ+3....(i)
3λ−1=2μ+k.....(ii)
4λ+1=μ....(iii)
has a unique solution.
Solving (i) and (iii), we get λ=−32,μ=−5
From (ii), we get −92−1=−10+k⇒k=92.
:
B
Any point onx−12=y+13=z−14=λ is,
(2λ+1,3λ−1,4λ+1);λ∈R
Any point on x−31=y−k2=z1=μ is,
(μ+3,2μ+k,μ);μ∈R
the given lines intersect if and only if the system of equations(in λ and μ)
2λ+1=μ+3....(i)
3λ−1=2μ+k.....(ii)
4λ+1=μ....(iii)
has a unique solution.
Solving (i) and (iii), we get λ=−32,μ=−5
From (ii), we get −92−1=−10+k⇒k=92.