Quantitative Aptitude
GEOMETRY MCQs
Coordinate Geometry, Coordinate Geometry (10th Grade), Three Dimensional Geometry (10th Grade)
Total Questions : 133
| Page 13 of 14 pages
Answer: Option A. -> √34
:
A
Perpendicular distance of (x,y,z) from y axis is given by =√x2+z2.
=>Required distance =√32+52=√34.
:
A
Perpendicular distance of (x,y,z) from y axis is given by =√x2+z2.
=>Required distance =√32+52=√34.
Answer: Option C. -> 5√2
:
C
Let the line segment be AB, then as given
ABcosα=3,ABcosβ=4,ABcosγ=5⇒AB2(cos2α+cos2β+cos2γ)=32+42+52AB=√9+16+25=5√2
where α,β and γare the angles made by the line with the axes.
:
C
Let the line segment be AB, then as given
ABcosα=3,ABcosβ=4,ABcosγ=5⇒AB2(cos2α+cos2β+cos2γ)=32+42+52AB=√9+16+25=5√2
where α,β and γare the angles made by the line with the axes.
Answer: Option A. -> 1
:
A
Line parallel to the line x2=y2=z−6 and passing through (1,-2, 3) is
x−12=y+23=z−3−6=r
A = (2r + 1, 3r – 2, – 6r + 3) is a point on this line.
A lies in the plane x – y + z = 5
∴2r+1−3r+2−6r+3=5⇒r=17∴A=(97,−117,157)
Distance of A from (1, –2, 3) is
√(97−1)2+(−117+2)2+(157−3)2=17√4+9+36=77=1
:
A
Line parallel to the line x2=y2=z−6 and passing through (1,-2, 3) is
x−12=y+23=z−3−6=r
A = (2r + 1, 3r – 2, – 6r + 3) is a point on this line.
A lies in the plane x – y + z = 5
∴2r+1−3r+2−6r+3=5⇒r=17∴A=(97,−117,157)
Distance of A from (1, –2, 3) is
√(97−1)2+(−117+2)2+(157−3)2=17√4+9+36=77=1
Answer: Option D. -> 2
:
D
Here, d1=dcos(90∘−α)
d2=dcos(90∘−β)
and d3=dcos(90∘−γ)
∴d1=dsinα
d2=dsinβ
and d3=dsinγ
∴d21+d22+d23=kd2
⇒d2(sin2α+sin2β+sin2γ)=k(d)2
∴k=2
:
D
Here, d1=dcos(90∘−α)
d2=dcos(90∘−β)
and d3=dcos(90∘−γ)
∴d1=dsinα
d2=dsinβ
and d3=dsinγ
∴d21+d22+d23=kd2
⇒d2(sin2α+sin2β+sin2γ)=k(d)2
∴k=2
Answer: Option D. -> 29x – 27y – 22z = 85
:
D
Equation of the plane through the point (2, –1, 0) is
a(x – 2) + b(y + 1) + c(z – 0) = 0 . . . (1)
It passes through the point (3, –4, 5)
∴a – 3b + 5c = 0 . . . (2)
The plane (1) is parallel to the line
2x = 3y = 4z i.e.,x6=y4=z3...(3)
∴ Normal to the plane (1) is perpendicular to the line (3).
∴6a + 4b + 3c = 0 . . .(4)
From (2) and (4), we get
a−29=b27=c22
∴ Equation of the required plane is
– 29(x – 2) + 27(y + 1) + 22(z) = 0
⇒−29x+27y+22z+85=0
⇒29x−27y−22z=85
:
D
Equation of the plane through the point (2, –1, 0) is
a(x – 2) + b(y + 1) + c(z – 0) = 0 . . . (1)
It passes through the point (3, –4, 5)
∴a – 3b + 5c = 0 . . . (2)
The plane (1) is parallel to the line
2x = 3y = 4z i.e.,x6=y4=z3...(3)
∴ Normal to the plane (1) is perpendicular to the line (3).
∴6a + 4b + 3c = 0 . . .(4)
From (2) and (4), we get
a−29=b27=c22
∴ Equation of the required plane is
– 29(x – 2) + 27(y + 1) + 22(z) = 0
⇒−29x+27y+22z+85=0
⇒29x−27y−22z=85
Answer: Option B. -> (3, -2, 1)
:
B
The straight line joining the points (1, 1, 2) and (3, -2, 1) is x−12=y−1−3=z−2−1=r (say)
∴ Point is (2r + 1, 1 -3r, 2 –r )
Which lies on 3x + 2y + z = 6
∴3(2r+1)+2(1−3r)+2−r=6
∴r=1
Required point is (3, -2, 1).
:
B
The straight line joining the points (1, 1, 2) and (3, -2, 1) is x−12=y−1−3=z−2−1=r (say)
∴ Point is (2r + 1, 1 -3r, 2 –r )
Which lies on 3x + 2y + z = 6
∴3(2r+1)+2(1−3r)+2−r=6
∴r=1
Required point is (3, -2, 1).
Answer: Option B. -> l1+l22cosθ2,m1+m22cosθ2,n1+n22cosθ2
:
B
Let OA and OB be two lines with d.c’s l1,m1,n1 and l2,m2,n2,. Let OA = OB = 1. Then, the coordinates of A and B are (l1,m1,n1) and (l2,m2,n2), respectively. Let OC be the bisector of ∠AOB .Then, C is the mid point of AB and so its coordinates are (l1+l22,m1+m22,n1+n22).
∴ d.r's of OC are l1+l22,m1+m22,n1+n22
We have, OC=√(l1+l22)2+(m1+m22)2+(n1+n22)2=12√(l21+m21+n21)+(l22+m22+n22)+(l1l2+m1m2+n1n2)=12√2+2cosθ[Qcosθ=l1l2+m1m2+n1n2]=12√2(1+cosθ)=cos(θ2)
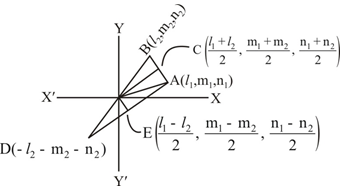
∴ d.c's of OC are
l1+l22(OC),m1+m22(OC),n1+n22(OC)
:
B
Let OA and OB be two lines with d.c’s l1,m1,n1 and l2,m2,n2,. Let OA = OB = 1. Then, the coordinates of A and B are (l1,m1,n1) and (l2,m2,n2), respectively. Let OC be the bisector of ∠AOB .Then, C is the mid point of AB and so its coordinates are (l1+l22,m1+m22,n1+n22).
∴ d.r's of OC are l1+l22,m1+m22,n1+n22
We have, OC=√(l1+l22)2+(m1+m22)2+(n1+n22)2=12√(l21+m21+n21)+(l22+m22+n22)+(l1l2+m1m2+n1n2)=12√2+2cosθ[Qcosθ=l1l2+m1m2+n1n2]=12√2(1+cosθ)=cos(θ2)

∴ d.c's of OC are
l1+l22(OC),m1+m22(OC),n1+n22(OC)
Answer: Option D. -> 6√2√13
:
D
Let equation of plane be lx + my + nz = p, where p is the perpendicular distance of the plane from origin and (l,m,n) are the direction cosines of the normal to the plane
Or x(pl)+y(pm)+z(pn)=1
According to question,
pl=12,pm=3,pn=4
or p12=l,p3=m,p4=n
or p2144+p29+p216=l2+m2+n2=1
⇒p2(1144+19+116)=1p2(1+16+9144)=1
Or p2=14426=7213
∴p=6√2√13
:
D
Let equation of plane be lx + my + nz = p, where p is the perpendicular distance of the plane from origin and (l,m,n) are the direction cosines of the normal to the plane
Or x(pl)+y(pm)+z(pn)=1
According to question,
pl=12,pm=3,pn=4
or p12=l,p3=m,p4=n
or p2144+p29+p216=l2+m2+n2=1
⇒p2(1144+19+116)=1p2(1+16+9144)=1
Or p2=14426=7213
∴p=6√2√13
Answer: Option A. -> x -2y -2z-3 =0, 2x+y -2z+3 =0
:
A
Equation of planes passing through intersection of the planes 3x-y-4z=0 and x+3y+6=0 is, (3x−y−4z)+λ(x+3y+6)=0.....(i)
Given, distance of plane (i) from origin is 1.
∴6λ√(3+λ)2+(3λ−1)2+42=1
or 36λ2=10λ2+26 or λ=±1
Put the value of λ in (i),
∴(3x−y−4z)±(x+3y+6)=0
or4x+2y -4z+6=0 i.e 2x+y-2z+3 =0
and 2x-4y-4z-6=0
Thus the required planes are x-2y-2z-3=0 and 2x+y-2z+3=0.
:
A
Equation of planes passing through intersection of the planes 3x-y-4z=0 and x+3y+6=0 is, (3x−y−4z)+λ(x+3y+6)=0.....(i)
Given, distance of plane (i) from origin is 1.
∴6λ√(3+λ)2+(3λ−1)2+42=1
or 36λ2=10λ2+26 or λ=±1
Put the value of λ in (i),
∴(3x−y−4z)±(x+3y+6)=0
or4x+2y -4z+6=0 i.e 2x+y-2z+3 =0
and 2x-4y-4z-6=0
Thus the required planes are x-2y-2z-3=0 and 2x+y-2z+3=0.
Answer: Option A. -> 2 : 3
:
A
let YZ-plane divide the segment joining (-2, 4, 7) and (3, -5, 8) in the ratio λ:1. Then ⇒3λ−2λ+1=0⇒λ=23 and the required ratio is 2 : 3
:
A
let YZ-plane divide the segment joining (-2, 4, 7) and (3, -5, 8) in the ratio λ:1. Then ⇒3λ−2λ+1=0⇒λ=23 and the required ratio is 2 : 3
















