Exams > Cat > Quantitaitve Aptitude
QUANTITAITVE APTITUDE CLUBBED MCQs
Total Questions : 1394
| Page 6 of 140 pages
Answer: Option D. -> 14,84
:
D
g(32)=1+2+4+8+16+32=63<2×32 (Category A)
g(64)=1+2+4+8+16+32+64=127<2×64 (Category A)
g(6)=1+2+3+6=12=2×6 (neither A nor B)
g(7)=1+7=8<2×7 (Category A)
g(28)=1+2+4+7+14+28=56=2×28 (Neither A nor B)
g(14)=1+2+7+14=24<2×14 (Category A)
g(84)=1+2+3+4+6+7+12+14+21+28+42+84=224>2×84 (Category B)
Hence, option (d).
:
D
g(32)=1+2+4+8+16+32=63<2×32 (Category A)
g(64)=1+2+4+8+16+32+64=127<2×64 (Category A)
g(6)=1+2+3+6=12=2×6 (neither A nor B)
g(7)=1+7=8<2×7 (Category A)
g(28)=1+2+4+7+14+28=56=2×28 (Neither A nor B)
g(14)=1+2+7+14=24<2×14 (Category A)
g(84)=1+2+3+4+6+7+12+14+21+28+42+84=224>2×84 (Category B)
Hence, option (d).
Answer: Option D. -> non - negative
:
D
Take any three consecutive natural numbers as: n-1, n, n + 1
Now add any two and subtract third from the sum.
n - 1 + n - (n + 1) = n - 2; n + n + 1 - (n - 1) = n + 2; n - 1 + n + 1 - n = n
So you will get either n - 2 or n + 2 or n. As you are considering natural numbers, smallest natural number is 1 ⟹ n -1 = 1 or n = 2. (So that n - 1 is a natural number)
So n - 2, n, n + 2 all three will be non - negative. So the given expression is also non - negative.
:
D
Take any three consecutive natural numbers as: n-1, n, n + 1
Now add any two and subtract third from the sum.
n - 1 + n - (n + 1) = n - 2; n + n + 1 - (n - 1) = n + 2; n - 1 + n + 1 - n = n
So you will get either n - 2 or n + 2 or n. As you are considering natural numbers, smallest natural number is 1 ⟹ n -1 = 1 or n = 2. (So that n - 1 is a natural number)
So n - 2, n, n + 2 all three will be non - negative. So the given expression is also non - negative.
:
P(A) = 13
P(A') = 23
P(Bird Killed) = 1 - P(None of 3 shots hit)
1− 23 ×23 × 23 = 1927
Answer: Option A. -> 2, 4 and 8
:
A
The sum of n consecutive odd numbers is given as n2 . Hence 1002 is divisible by 2, 4 and 8. Answer is option (a).
(Sum of n consecutive odd numbers =n2 is derived from unitary method as follows : 1 + 3 + 5 + 7 + 9 +...... is a series (AP) with a common difference of 2. Therefore, the 100th term would be 99×2+1= 199. Therefore the sum = (1+199)1002=10000 or n2.
:
A
The sum of n consecutive odd numbers is given as n2 . Hence 1002 is divisible by 2, 4 and 8. Answer is option (a).
(Sum of n consecutive odd numbers =n2 is derived from unitary method as follows : 1 + 3 + 5 + 7 + 9 +...... is a series (AP) with a common difference of 2. Therefore, the 100th term would be 99×2+1= 199. Therefore the sum = (1+199)1002=10000 or n2.
Answer: Option C. -> 4sq units
:
C
Approach 1:
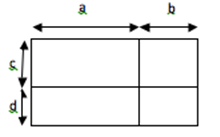
You can directly mark the answer as 25 × x = 20 × 5 ⇒ x=4
Proof:
Observe that
ac = 25 sq units ....(1)
bc= 20 sq units ... (2)
ad = 5 sq units ... (3)
Dividing (1) by (3), we get: cd = 5 units ... (4)
Dividing (1) by (2) we get ab =5/4 units ... (5)
St Multiplying (4) and (5) we get:
Sit acbd = 254 sq units
Since its already given that ac = 25 sq units, therefore the missing area 'X' =4 square units.
Approach 2:
Use the simple number approach to break up the values in each cell as shown below
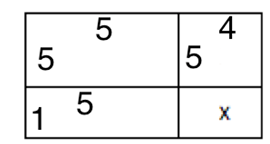
thus x=4x1=4
:
C
Approach 1:

You can directly mark the answer as 25 × x = 20 × 5 ⇒ x=4
Proof:
Observe that
ac = 25 sq units ....(1)
bc= 20 sq units ... (2)
ad = 5 sq units ... (3)
Dividing (1) by (3), we get: cd = 5 units ... (4)
Dividing (1) by (2) we get ab =5/4 units ... (5)
St Multiplying (4) and (5) we get:
Sit acbd = 254 sq units
Since its already given that ac = 25 sq units, therefore the missing area 'X' =4 square units.
Approach 2:
Use the simple number approach to break up the values in each cell as shown below

thus x=4x1=4
Answer: Option B. -> 3
:
B
To write a number as a difference of squares of 2 natural numbers, we need to find the 2 factor products of the number, such that both the factors are either even or odd.
This is because if we are writing a number N as a difference of squares, then -
N=a2−b2⟹N=(a+b)(a−b). If (a+b, a-b) is a pair of one odd and one even number, 'a' and 'b' can't be natural numbers.
Hence, both the factors need to be either even or odd.
In the case of 80, the possible cases are 80=2×40;=4×20;=8×10.
Thus, there are only three instances where both are even. Hence, the answer is option (b).
:
B
To write a number as a difference of squares of 2 natural numbers, we need to find the 2 factor products of the number, such that both the factors are either even or odd.
This is because if we are writing a number N as a difference of squares, then -
N=a2−b2⟹N=(a+b)(a−b). If (a+b, a-b) is a pair of one odd and one even number, 'a' and 'b' can't be natural numbers.
Hence, both the factors need to be either even or odd.
In the case of 80, the possible cases are 80=2×40;=4×20;=8×10.
Thus, there are only three instances where both are even. Hence, the answer is option (b).
Question 58. There are some boxes labelled 1, 2, 3, 4... and so on up to 2n, where n>6 such that, for k = 1, 2, 3, 4, .... 2n, there are exactly k boxes labelled k. The total number of boxes is N. Now, consider the following two cases for the number of footballs (fi) in the box labelled i:
Case 1: fi=i+1, if i is odd; = i + 2 if i is even.
Case 2: fi=i+2, if i is odd; = i + 1 if i is even.
The difference between the total number of footballs in the N boxes in Case 1 and Case 2 is:
Case 1: fi=i+1, if i is odd; = i + 2 if i is even.
Case 2: fi=i+2, if i is odd; = i + 1 if i is even.
The difference between the total number of footballs in the N boxes in Case 1 and Case 2 is:
Answer: Option B. -> √8N+1−14
:
B
Method 1- Conventional Approach
Clearly, in both cases, fi=(i+1) or (i+1) + 1.
Therefore in both the cases, (i+1) is common.
As we need to find the difference in number of footballs, we can ignore (i+1).
Thus, effectively in each box, there will be 0 or 1 football.
We get:
Case 1: fi=0 if i is odd, = 1 if i is even.
Case 2: fi=1 if i is odd, = 0 if i is even.
Upon observation, we can conclude that the required difference is nothing but the difference in the number of boxes with odd numbered labels and the number of boxes with even numbered labels.
Also, number of boxes with label (x) is 1 more than number of boxes with label (x-1).
From 2n labels, we get n pairs of labels with consecutive numbers.
Therefore, required difference is n×1=n.
Or Case 1 - Case 2 = [{2+4+6+....+(2n)}-{1+3+5+....+(2n-1)}]
=2n(n+1)2−n2=n
Total number of boxes = 1+2+3+....+2n= n(2n+1) = N
Therefore, 2n2+n−N=0
n=−1±√1+8N4
Since n cannot be negative, n=(√8N+1)−14.
Therefore, answer option (b) is the correct answer choice.
Method 2- Assumption
This is a question based on Variables to Variables.
Assume n=1, hence the number of boxes labelled 1, will be 1 and the number of boxes labelled 2 will be 2. Total number of boxes (N) = 3.
Case 1
When i=1,f1=2 and when i=2,f2=4
Case 2
When i=1,f1=3 and when i=2,f2=3
Difference in total number of footballs in both cases = (2+4+4) - (3+3+3) = 1
Now, on substitution of N=3 in options, eliminate those options where you are not getting 1.
Only option (b) satisfies the required condition.
:
B
Method 1- Conventional Approach
Clearly, in both cases, fi=(i+1) or (i+1) + 1.
Therefore in both the cases, (i+1) is common.
As we need to find the difference in number of footballs, we can ignore (i+1).
Thus, effectively in each box, there will be 0 or 1 football.
We get:
Case 1: fi=0 if i is odd, = 1 if i is even.
Case 2: fi=1 if i is odd, = 0 if i is even.
Upon observation, we can conclude that the required difference is nothing but the difference in the number of boxes with odd numbered labels and the number of boxes with even numbered labels.
Also, number of boxes with label (x) is 1 more than number of boxes with label (x-1).
From 2n labels, we get n pairs of labels with consecutive numbers.
Therefore, required difference is n×1=n.
Or Case 1 - Case 2 = [{2+4+6+....+(2n)}-{1+3+5+....+(2n-1)}]
=2n(n+1)2−n2=n
Total number of boxes = 1+2+3+....+2n= n(2n+1) = N
Therefore, 2n2+n−N=0
n=−1±√1+8N4
Since n cannot be negative, n=(√8N+1)−14.
Therefore, answer option (b) is the correct answer choice.
Method 2- Assumption
This is a question based on Variables to Variables.
Assume n=1, hence the number of boxes labelled 1, will be 1 and the number of boxes labelled 2 will be 2. Total number of boxes (N) = 3.
Case 1
When i=1,f1=2 and when i=2,f2=4
Case 2
When i=1,f1=3 and when i=2,f2=3
Difference in total number of footballs in both cases = (2+4+4) - (3+3+3) = 1
Now, on substitution of N=3 in options, eliminate those options where you are not getting 1.
Only option (b) satisfies the required condition.
Answer: Option D. -> 100
:
D
The minimum value of such an expression occurs when x takes the middle value in the given range i.e. when x is between 10 and 11. And the value of the function f(x) at that value becomes:
f(x=10) = 9+8+7+6+5+4+3+2+1+0+1+2+3+4+5+6+7+8+9+10 = 100
Also,f(x=11) = 10+9+8+7+6+5+4+3+2+1+0+1+2+3+4+5+6+7+8+9=100
Therefore, answer option (d) stands out as the correct answer choice.
:
D
The minimum value of such an expression occurs when x takes the middle value in the given range i.e. when x is between 10 and 11. And the value of the function f(x) at that value becomes:
f(x=10) = 9+8+7+6+5+4+3+2+1+0+1+2+3+4+5+6+7+8+9+10 = 100
Also,f(x=11) = 10+9+8+7+6+5+4+3+2+1+0+1+2+3+4+5+6+7+8+9=100
Therefore, answer option (d) stands out as the correct answer choice.
Answer: Option D. -> 8
:
D
The sum of even, odd, even is odd and the sum of odd, even, odd is even. To get an even sum, the three consecutive integers are odd, even, and odd (or) should start with odd. Hence we have 1 + 2+ 3 = 6 which is 6 less than 3 + 4 + 5 = 12 since 3 is 2 more than 1, 4 is 2 more than 2 and 5 is 2 more than 3. Therefore 5 + 6 + 7 is 6 more than 3 + 4 + 5. Hence we get all multiples of 6 less than 50. They are 6,12,18,24,30,36,42,48.
Hence option (d) is the correct choice.
Alternate Solution:
Let the three consecutive integers be (a-1), (a), (a+1).
(a - 1) + a + (a + 1) = 3a = 50. So all even multiples of 3 which are less than 50, can be written in the form of 3 consecutive integers.
:
D
The sum of even, odd, even is odd and the sum of odd, even, odd is even. To get an even sum, the three consecutive integers are odd, even, and odd (or) should start with odd. Hence we have 1 + 2+ 3 = 6 which is 6 less than 3 + 4 + 5 = 12 since 3 is 2 more than 1, 4 is 2 more than 2 and 5 is 2 more than 3. Therefore 5 + 6 + 7 is 6 more than 3 + 4 + 5. Hence we get all multiples of 6 less than 50. They are 6,12,18,24,30,36,42,48.
Hence option (d) is the correct choice.
Alternate Solution:
Let the three consecutive integers be (a-1), (a), (a+1).
(a - 1) + a + (a + 1) = 3a = 50. So all even multiples of 3 which are less than 50, can be written in the form of 3 consecutive integers.
















