Exams > Cat > Quantitaitve Aptitude
QUANTITAITVE APTITUDE CLUBBED MCQs
Total Questions : 1394
| Page 1 of 140 pages
Answer: Option C. -> 8455680
:
C
Total number of combinations = No repeats + 1 number repeat + 2 number repeat +.....7 number repeat
Total number of combinations - No repeats = 1 number repeat + 2 number repeat +...... 7 number repeat
Total number of combinations - No repeats = Atleast one number repeat
106×9−(9.9.8.7.6.5.4)=9000000−544320=8455680
:
C
Total number of combinations = No repeats + 1 number repeat + 2 number repeat +.....7 number repeat
Total number of combinations - No repeats = 1 number repeat + 2 number repeat +...... 7 number repeat
Total number of combinations - No repeats = Atleast one number repeat
106×9−(9.9.8.7.6.5.4)=9000000−544320=8455680
Answer: Option B. -> 22
:
B
⇒([1p]+p)2 = 9
⇒([1p2]+p2+2) = 9
⇒([1p2]+p2) = 7
Circumference = 2πr ≈ 22
:
B
⇒([1p]+p)2 = 9
⇒([1p2]+p2+2) = 9
⇒([1p2]+p2) = 7
Circumference = 2πr ≈ 22
Answer: Option C. -> 87
:
C
The sum has to end with a zero. The numbers have to end with 7,9,1,3. Option (d) is out. Go from answer options, answer is option (c).
The numbers are 87, 89, 91, 93 which add up to 360. 36 is a perfect square.
:
C
The sum has to end with a zero. The numbers have to end with 7,9,1,3. Option (d) is out. Go from answer options, answer is option (c).
The numbers are 87, 89, 91, 93 which add up to 360. 36 is a perfect square.
Question 4. Given that: Side of square ABCD = 4cm, E, F, G and H are midpoints of the sides AD, AB, BC and CD respectively. Also, the line passing through ON would bisect the line XF. Similar is the case for all other pairs: PO, RS and TM. Lastly, the lengths TM = NO = PQ = RS = 14 side of square (Note: The figure given below is a symmetric figure). X is the centre point of the square. The area of the shaded region is ___
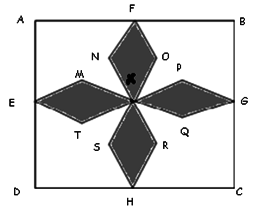

:
Using graphical division, we can divide the figure to look like the following:
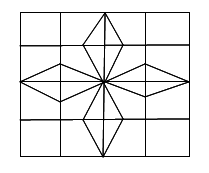
Looking at the figure, we can easily make out that the shaded region is made out of 16 triangles,
Each being 1/64th the size of the larger square. (Since, area of each triangle =14 * 116 is area of square)
Therefore, area of shaded region = (14×116×16×16)cm2
Thus, required area of shaded region = 4cm2.
Answer: Option A. -> pq2
:
A
Since the only condition we need to maintain is that the diagonals need to intersect at right angles, assume the simplest quadrilateral which satisfies this condition- a square. Now the question can be solved by simple graphical division.
Take the side of the square =p=q=2. Area = 4.
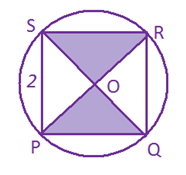
We need the area of the shaded region, which is half of that of the square= 2. Look in the answer options for 2 on substituting p=2 and q=2. Answer is option (a)
:
A
Since the only condition we need to maintain is that the diagonals need to intersect at right angles, assume the simplest quadrilateral which satisfies this condition- a square. Now the question can be solved by simple graphical division.
Take the side of the square =p=q=2. Area = 4.
We need the area of the shaded region, which is half of that of the square= 2. Look in the answer options for 2 on substituting p=2 and q=2. Answer is option (a)
Answer: Option C. -> 7
:
C
Express the power in the form of 4K + X. In this case 797 = 4K + 1.
159871 = Unit digit is 7. Hence, remainder is 7 when divided by 10.
:
C
Express the power in the form of 4K + X. In this case 797 = 4K + 1.
159871 = Unit digit is 7. Hence, remainder is 7 when divided by 10.
Answer: Option D. -> 8
:
D
f(a).f(b).f(c) = (6−a)(6−b)(6−c)abc = 216−36(a+b+c)+6(ab+bc+ca)−abcabc = (ab+bc+ca)abc - 1 = 6(1a+1b+1c) - 1
As AM≥HM
(1a+1b+1c)3 = 6a+6b+6c3 > 3
6a+6b+6c > 9
f(a).f(b).f(c)> 9 - 1 = 8
:
D
f(a).f(b).f(c) = (6−a)(6−b)(6−c)abc = 216−36(a+b+c)+6(ab+bc+ca)−abcabc = (ab+bc+ca)abc - 1 = 6(1a+1b+1c) - 1
As AM≥HM
(1a+1b+1c)3 = 6a+6b+6c3 > 3
6a+6b+6c > 9
f(a).f(b).f(c)> 9 - 1 = 8
Answer: Option C. -> 10.5
:
C
Multiply both equations - (a+b)(c +d) = 10
⟹ ac+bd=8 (ad=bc=1)...(i)
a(c+d)=2a (c+d=2)
⟹ ac+ad=ac+bc=c(a+b)=2a
⟹ac=52...(ii)
Hence (i)+(ii) = ac+bd+(ac) = 8+52=10.5
:
C
Multiply both equations - (a+b)(c +d) = 10
⟹ ac+bd=8 (ad=bc=1)...(i)
a(c+d)=2a (c+d=2)
⟹ ac+ad=ac+bc=c(a+b)=2a
⟹ac=52...(ii)
Hence (i)+(ii) = ac+bd+(ac) = 8+52=10.5
Answer: Option B. -> 3456
:
B
If all the digits are different, and there are 10 of them, then all the digits from 0 to 9 must appear.
That implies that the digits of abcdefghij add up to 45 =0+1+2+3+...+9.
That implies that abcdefgh is definitely divisible by 9.
Since 9 and 1 1 1 1 1 are relatively prime, their least common multiple is 9×11111=99999,
Thus abcdefgh must be divisible by 99999.
We have to find the condition such that abcdefghij is divisible by 99999.
abcdefghij =abcde×105+ fghij and, this number is exactly divisible by(105-1).
Hence by remainder theorem, (abcde×105+ fghij) must be 99999.
Then the following equations must all hold:
f =9-a, g =9-b,h =9-c, I =9-d, j =9-c
Now there are 9 Options for a (it can't be 0) and then f is known.That leaves 8 options for b, and
then'g' is known. That leaves 6 Options for c, and then h is known.
That leaves 4 Options for d and then I is known.
That leaves 2 Options for c, and then j is known.
Thus, the total number of such number abcdefghij is 9×8×6×4×2=3456.
:
B
If all the digits are different, and there are 10 of them, then all the digits from 0 to 9 must appear.
That implies that the digits of abcdefghij add up to 45 =0+1+2+3+...+9.
That implies that abcdefgh is definitely divisible by 9.
Since 9 and 1 1 1 1 1 are relatively prime, their least common multiple is 9×11111=99999,
Thus abcdefgh must be divisible by 99999.
We have to find the condition such that abcdefghij is divisible by 99999.
abcdefghij =abcde×105+ fghij and, this number is exactly divisible by(105-1).
Hence by remainder theorem, (abcde×105+ fghij) must be 99999.
Then the following equations must all hold:
f =9-a, g =9-b,h =9-c, I =9-d, j =9-c
Now there are 9 Options for a (it can't be 0) and then f is known.That leaves 8 options for b, and
then'g' is known. That leaves 6 Options for c, and then h is known.
That leaves 4 Options for d and then I is known.
That leaves 2 Options for c, and then j is known.
Thus, the total number of such number abcdefghij is 9×8×6×4×2=3456.
Answer: Option B. -> 1
:
B
option (b)
On the first day there will be three balls, on second day there will be 9, on the third day 27.
Therefore on the 28th day =328balls.We need to find the remainder when divided by 5, 28= 4k. Therefore, 1 ball will be thrown away.
:
B
option (b)
On the first day there will be three balls, on second day there will be 9, on the third day 27.
Therefore on the 28th day =328balls.We need to find the remainder when divided by 5, 28= 4k. Therefore, 1 ball will be thrown away.