12th Grade > Mathematics
LIMITS CONTINUITY AND DIFFERENTIABILITY MCQs
Total Questions : 45
| Page 4 of 5 pages
Answer: Option C. -> ba
:
C
limx→0xa[bx]
=limx→0xa(bx−{bx})
Since {bx}ϵ[0,1)
=limx→0xa.{bx}=0
limx→0xa[bx]=limx→0(xa)(bx)
=limx→0.ba
=ba
:
C
limx→0xa[bx]
=limx→0xa(bx−{bx})
Since {bx}ϵ[0,1)
=limx→0xa.{bx}=0
limx→0xa[bx]=limx→0(xa)(bx)
=limx→0.ba
=ba
Answer: Option A. -> 1
:
A
limx→02sinx−sin2xx3
=limx→02sinx(1−cosx)(1+cosx)x3(1+cosx)
=limx→02sin3xx3×11+cosx
=2×(1)3×11+1=1
:
A
limx→02sinx−sin2xx3
=limx→02sinx(1−cosx)(1+cosx)x3(1+cosx)
=limx→02sin3xx3×11+cosx
=2×(1)3×11+1=1
Answer: Option C. -> 1
:
C
limx→∞x+cosxx+sinx[Puttingx=1h;asx→∞,h→0]=limh→01h+cos(1h)1h+sin(1h)=limh→01+hcos1h1+hcos1h=1+01+0⎡⎢
⎢
⎢⎣∵−1≤sin1h≤1and−1≤cos1h≤1,∴whereh→0,hcos1h→0andhsin1h→0⎤⎥
⎥
⎥⎦=1
:
C
limx→∞x+cosxx+sinx[Puttingx=1h;asx→∞,h→0]=limh→01h+cos(1h)1h+sin(1h)=limh→01+hcos1h1+hcos1h=1+01+0⎡⎢
⎢
⎢⎣∵−1≤sin1h≤1and−1≤cos1h≤1,∴whereh→0,hcos1h→0andhsin1h→0⎤⎥
⎥
⎥⎦=1
Answer: Option C. -> 1
:
C
limx→0kx cosec x = limx→0 x cosec kx
= k limx→0xsinx =1klimx→0kxsinkx =k=1k=k=± 1
:
C
limx→0kx cosec x = limx→0 x cosec kx
= k limx→0xsinx =1klimx→0kxsinkx =k=1k=k=± 1
Answer: Option B. -> -1/2
:
B
limx→0tan−1x−sin−1xx3(00form)limx→011+x2−1√1−x23x2limx→0√1−x2−(1+x2)3x2(1+x2)√1−x2limx→0(1−x2)−(1+x2)23x2(1+x2)√1−x2[√1−x2+(1+x2)]=−36=−12
:
B
limx→0tan−1x−sin−1xx3(00form)limx→011+x2−1√1−x23x2limx→0√1−x2−(1+x2)3x2(1+x2)√1−x2limx→0(1−x2)−(1+x2)23x2(1+x2)√1−x2[√1−x2+(1+x2)]=−36=−12
Answer: Option A. -> 2/3
:
A
limx→0(1+x)13−(1−x)13x=limx→0(1+x)13−(1−x)13(1+x)−(1−x).2=2.13
:
A
limx→0(1+x)13−(1−x)13x=limx→0(1+x)13−(1−x)13(1+x)−(1−x).2=2.13
Answer: Option C. -> 1128r
:
C
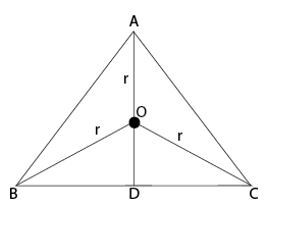
In △ABC,AB=AC
AD⊥BC(DismidpointofBC)
Let r = radius of circumcircle
⇒OA = OB = OC = r
Now BD = √BO2−OD2
=√r2−(h−r)2=√2rh−h2
⇒BC=2√2rh−h2
∴ Area of △ABC= 12×BC×AD
=h√2rh−h2
Also limh→0Ap3=h√2rh−h28(√2rh−h2+√2hr)3
=limh→0h3/2√2r−h8h3/2(√2r−h+√2r)3
=limh→0√2r−h8[√2r−h+√2r]3
=√2r8(√2r+√2r)3=√2r8.8.2r√2r=1128r
:
C
In △ABC,AB=AC
AD⊥BC(DismidpointofBC)
Let r = radius of circumcircle
⇒OA = OB = OC = r
Now BD = √BO2−OD2
=√r2−(h−r)2=√2rh−h2
⇒BC=2√2rh−h2
∴ Area of △ABC= 12×BC×AD
=h√2rh−h2
Also limh→0Ap3=h√2rh−h28(√2rh−h2+√2hr)3
=limh→0h3/2√2r−h8h3/2(√2r−h+√2r)3
=limh→0√2r−h8[√2r−h+√2r]3
=√2r8(√2r+√2r)3=√2r8.8.2r√2r=1128r
Answer: Option C. -> 27
:
C
f′(x)=limh→0f(x+h)−f(x)h
=limh→0f(x)+f(h)−f(x)h
=limh→0(2h2+3h)g(h)h
=limh→0(2h+3)g(h)
=3g(0)
=27
:
C
f′(x)=limh→0f(x+h)−f(x)h
=limh→0f(x)+f(h)−f(x)h
=limh→0(2h2+3h)g(h)h
=limh→0(2h+3)g(h)
=3g(0)
=27
Answer: Option A. -> a=1,b=−32
:
A
limx→∞(x2+1x+1−ax−b)=12⇒limx→∞(x2+1)−(ax+b)(x+1)x+1=12⇒limx→∞x2(1−a)−(a+b)x−b+1x+1=12⇒1−a=0anda+b=−12∴a=1b=−32
:
A
limx→∞(x2+1x+1−ax−b)=12⇒limx→∞(x2+1)−(ax+b)(x+1)x+1=12⇒limx→∞x2(1−a)−(a+b)x−b+1x+1=12⇒1−a=0anda+b=−12∴a=1b=−32
Answer: Option A. -> a = 2, b = 3
:
A
Wehave,f(x)={ax2+b,x<−1bx2+ax+4,x≥−1∴f′(x)={2ax,<−12bx+a,x≥−1Since,f(x)isdifferentiableatx=−1,thereforeitiscontinuousatx=−1andhence,limx→−1−f(x)=limx→−1+f(x)⇒a+b=b−a+4⇒a=2andalso,limx→−1−f(x)=limx→−1+f(x)⇒−2a=−2b+a⇒3a=2b⇒b=3(∵a=2)Hence,a=2,b=3
:
A
Wehave,f(x)={ax2+b,x<−1bx2+ax+4,x≥−1∴f′(x)={2ax,<−12bx+a,x≥−1Since,f(x)isdifferentiableatx=−1,thereforeitiscontinuousatx=−1andhence,limx→−1−f(x)=limx→−1+f(x)⇒a+b=b−a+4⇒a=2andalso,limx→−1−f(x)=limx→−1+f(x)⇒−2a=−2b+a⇒3a=2b⇒b=3(∵a=2)Hence,a=2,b=3
Latest Videos
Latest Test Papers
Login With Google
Old way of Login
Login With Email