Question
PQRS is a square of length x, a natural number >1. Let L1,L2,L3,L4…be points on QR such that QL1=L1L2=L2L3=L3L4….=1 and M1,M2,M3 be points on RS such that R\(M_1=M_1M_2=M_2M_3. . . . . . .=1\). Then, a−1n−1∑(PL2n+LnM2n) is equal to?
Answer: Option B
:
B
Option (b)
Assume a square of side 2 as follows with L1 as the midpoint of side QR and M1 as the mid-point of side RS
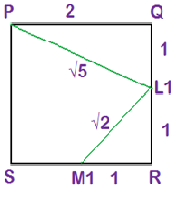
At n=1, the expression yields a value 5+2=7
Look in the answer options for 7, when n=1. Eliminate those answer options where this is not obtained
12*a*(a-1)2= 1
12 *a*(a-1)*(4a-1)= 7
12 *(a-1)*(2a-1)*(4a-1)= 212
12*(a+1)*(2a-1)*(4a-1)= 632
a2*2n2 = 8
Was this answer helpful ?
:
B
Option (b)
Assume a square of side 2 as follows with L1 as the midpoint of side QR and M1 as the mid-point of side RS
At n=1, the expression yields a value 5+2=7
Look in the answer options for 7, when n=1. Eliminate those answer options where this is not obtained
12*a*(a-1)2= 1
12 *a*(a-1)*(4a-1)= 7
12 *(a-1)*(2a-1)*(4a-1)= 212
12*(a+1)*(2a-1)*(4a-1)= 632
a2*2n2 = 8
Was this answer helpful ?
More Questions on This Topic :
Latest Videos
Latest Test Papers
Submit Solution