Question
If the graph of the function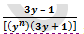 is symmetric about the y axis then determine the possible value of ‘n.’
is symmetric about the y axis then determine the possible value of ‘n.’
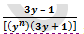 is symmetric about the y axis then determine the possible value of ‘n.’
is symmetric about the y axis then determine the possible value of ‘n.’
Answer: Option C
:
C
Soln:
f(y) = (3y – 1)/[(yn)(3y + 1)] = [1/(yn)][ (3y – 1)/(3y + 1)] = h(y) g(y)
Consider g(y) = (3y – 1)/(3y + 1)
g(-y)= (3-y – 1)/(3-y + 1)= (1 – 3y)/(1 + 3y) = -g(y)
So, g(y) is an odd function.
Now, as f(y) is symmetric about the y axis, f(y) is an even function.
h(y)*odd function = even function
→h(y) should be an odd function
h(y) = 1/yn
for h(y) to be odd, n has to be odd.
Hence option (c)
Shortcut
Put y=1 and y=-1, since it is mentioned that it is symmetric about the y axis. The values of both expressions should be equal. This will happen only if n is odd. Hence the answer is option (c)
Was this answer helpful ?
:
C
Soln:
f(y) = (3y – 1)/[(yn)(3y + 1)] = [1/(yn)][ (3y – 1)/(3y + 1)] = h(y) g(y)
Consider g(y) = (3y – 1)/(3y + 1)
g(-y)= (3-y – 1)/(3-y + 1)= (1 – 3y)/(1 + 3y) = -g(y)
So, g(y) is an odd function.
Now, as f(y) is symmetric about the y axis, f(y) is an even function.
h(y)*odd function = even function
→h(y) should be an odd function
h(y) = 1/yn
for h(y) to be odd, n has to be odd.
Hence option (c)
Shortcut
Put y=1 and y=-1, since it is mentioned that it is symmetric about the y axis. The values of both expressions should be equal. This will happen only if n is odd. Hence the answer is option (c)
Was this answer helpful ?


















Submit Solution