Geometry Set I(Exams > Cat > Quantitaitve Aptitude ) Questions and answers for exam Preparation

Exams > Cat > Quantitaitve Aptitude

GEOMETRY SET I MCQs

Total Questions : 110 | Page 1 of 11 pages

Question 1. Find the slope of the line joining the points (7, 5) and (9, 7):

Discuss Question

Answer: Option A. -> 1
:
A
Option(a)
Slope of the line =

\frac{y_{2} - y_{1}}{x_{2} - x_{1}} = \frac{7 - 5}{9 - 7} = 1

Here

(x_{1}, y_{1})

= (7, 5) and

(x_{2}, y_{2})

= (9, 7)

Question 2. Find the area of pentagon formed by joining the points (4, 4), (2, 2), (6, 2), (2, - 3) and (6, -3):

Discuss Question

Answer: Option A. -> 24
:
A

Find The Area Of Pentagon Formed By Joining The Points (4, 4...

Area of pentagon = Area of triangle ABE + Area of rectangle BCDE

\frac{1}{2} \times 4 \times 2 + 5 \times 4 = 24

Question 3. The lines 2x + 2y + 1 = 0 and 8x – 2y + 9 = 0 intersect in the

1st quadrant
2nd quadrant
3rd quadrant
4th quadrant

Discuss Question

Answer: Option B. -> 2nd quadrant
:
B
2x + 2y + 1 = 0 …………….(i)
8x – 2y + 9 = 0 …………………………(ii)
After solving equation (i) and (ii)
x = - 1 and y =

\frac{1}{2}

(- 1, \frac{1}{2})

; which is in

2^{n d}

quadrant.

Question 4. Determine the radius of the circle, two of whose tangents are the lines 2x+3y-9 = 0 and 4x+6y+19 =0

134√37
354√13
114√13
374√13

Discuss Question

Answer: Option D. -> 374√13
:
D
The given tangents are
2x+3y-9 = 0
4x+6y+19 =0
Or 2x + 3y +

\frac{19}{2}

= 0
Which are parallel, than distance between parallel tangents must be diameter of the circle than diameter.

\frac{∣ ∣ ∣ \frac{19}{2} - (- 9) ∣ ∣ ∣}{\sqrt{2^{2} + 3^{2}}} = \frac{37}{2 \sqrt{13}}

Radius =

\frac{1}{2}

diameter =

\frac{37}{4 \sqrt{13}}

Question 5. Three points A, B and C are collinear such that AB = 2BC. If the coordinates of the points A and B are (1, 7) and (6, -3) respectively, then the coordinates of the point C can be

(72;−2)
(172;−8)
(−172;−8)
(172;−2)

Discuss Question

Answer: Option B. -> (172;−8)
:
B
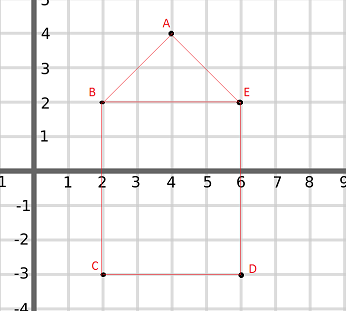
Given, AB = 2BC
AB : BC = 2 : 1
Let C BE (h, k), then

(\frac{2 h \pm 1}{2 \pm 1}; \frac{2 k \pm 7}{2 \pm 1})

= (6, - 3) [B may divide AC internally or externally]
2h + 1 = 18 and 2k + 7 = - 9
(or) 2h - 1 = 6 , 2k - 7 = - 3
2h = 17 and 2k = - 16 (or) 2h = 7, 2k = 4
h =

\frac{17}{2}

and k = - 8 (or) h =

\frac{7}{2}

; k = 2
C =

(\frac{17}{2}; - 8)

(\frac{17}{2}; 2)

Option(b)

Question 6. Let

α

β

be such that

π

< (

α

β

) < 3

π

. If sin

α

+ sin

β

= -

\frac{21}{65}

and cos

α

+ cos

β

= -

\frac{27}{65}

, then the value of \
cos

\frac{α - β}{2}

−665
3√130
665
-3√130

Discuss Question

Answer: Option D. -> -3√130
:
D
(d)sin

α

+ sin

β

= -

\frac{21}{65}

, cos

α

+ cos

β

= -

\frac{27}{65}

Now (sin

α

+ sin

β

)

^{2}

+ (cos

α

+ cos

β

)

^{2}

{(- \frac{21}{65})}^{2}

{(- \frac{27}{65})}^{2}

\Rightarrow

2 + 2 sin

α

sin

β

+ 2 cos

α

cos

β

\frac{441}{65^{2}}

\frac{729}{65^{2}}

\Rightarrow

2 + 2[cos (

α

β

)] =

\frac{1170}{(65)^{2}}

\Rightarrow

2.2 cos

^{2}

(\frac{α + β}{2}) = \frac{1170}{(65)^{2}}

\Rightarrow

cos

(\frac{α - β}{2})

\frac{3 \sqrt{130}}{130}

\frac{3}{\sqrt{130}}

Therefore cos

(\frac{α - β}{2})

\frac{- 3}{\sqrt{130}}

{

∵

\frac{π}{2}

\frac{α - β}{2}

\frac{3 π}{2}

}

Question 7. Let A

_{0}

_{1}

_{2}

_{3}

_{4}

_{5}

be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths of the line segments A

_{0}

_{1}

, A

_{0}

_{2}

and A

_{0}

_{4}

34
3√3
3
3√32

Discuss Question

Answer: Option C. -> 3
:
C
(c) Each triangle is an equilateral triangle

Let A0A1A2A3A4A5 Be A Regular Hexagon Inscribed In A Circle ...

Hence A

_{0}

_{1}

= 1
A

_{0}

_{0}^{2}

_{0}

_{1}^{2}

_{1}

_{0}^{2}

- 2A

_{0}

_{1}

_{1}

_{2}

cos 120

^{\circ}

= 1 + 1 - 2.1.1(-

\frac{1}{2}

) = 3

\Rightarrow

_{0}

_{2}

\sqrt{3}

_{0}

_{4}

∴

_{0}

_{1}

\times

_{0}

_{2}

\times

_{0}

_{4}

= 1.

\sqrt{3}

\sqrt{3}

Question 8. The maximum value of cos

α_{1}

.cos

α_{2}

........cos

α_{n}

, under the restrictions 0

\leq

α_{1}

α_{2}

,.........

α_{n}

\leq

\frac{π}{2}

and
cot

α_{1}

.cot

α_{2}

........cot

α_{n}

= 1 is

12n/2
12n
12n
1

Discuss Question

Answer: Option A. -> 12n/2
:
A
(a) Here (cot

α_{1}

).(cot

α_{2}

)....(cot

α_{n}

)= 1

∴

cos

α_{1}

.cos

α_{2}

........cos

α_{n}

= sin

α_{1}

.sin

α_{2}

........sin

α_{n}

Now, (cos

α_{1}

.cos

α_{2}

........cos

α_{n}

)

^{2}

= (cos

α_{1}

.cos

α_{2}

........cos

α_{n}

) (cos

α_{1}

.cos

α_{2}

........cos

α_{n}

)
= (cos

α_{1}

.cos

α_{2}

........cos

α_{n}

) (sin

α_{1}

.sin

α_{2}

........sin

α_{n}

)
=

\frac{1}{2^{n}}

sin 2

α_{1}

.sin 2

α_{2}

........sin 2

α_{n}

But each of sin 2

α_{i}

\leq

1
(cos

α_{1}

.cos

α_{2}

........cos

α_{n}

)

^{2}

\leq

\frac{1}{2^{n}}

But each of cos

α_{i}

, is positive.

∴

cos

α_{1}

.cos

α_{2}

........cos

α_{n}

\leq

\sqrt{\frac{1}{2^{n}}}

\frac{1}{2^{n / 2}}

Question 9. If

α

β

γ

δ

are the smallest positive angles in ascending order of magnitude which have their sines equal to the positive
quantity k, then the value of 4 sin

\frac{α}{2}

+ 3 sin

\frac{β}{2}

+ 2 sin

\frac{γ}{2}

+ sin

\frac{δ}{2}

is equal to

2√1−k
12√1+k.
2√1+k.
None of these

Discuss Question

Answer: Option C. -> 2√1+k.
:
C
(c) Given

α

β

γ

δ

and sin

α

= sin

β

= sin

γ

= sin

δ

= k. Also

α

β

γ

δ

are smallest positive angles satisfying above two conditions.

∴

We can take

β

π

α

γ

= 2

π

α

δ

= 3

π

α

Given expression
= 4 sin

\frac{α}{2}

+ 3 sin

(\frac{π}{2} - \frac{α}{2})

+ 2 sin

(π + \frac{α}{2})

+3 sin

(\frac{3 π}{2} - \frac{α}{2})

=4 sin

\frac{α}{2}

+ 3cos

\frac{α}{2}

- 2sin

\frac{α}{2}

-cos

\frac{α}{2}

= 2

(sin \frac{α}{2} + cos \frac{α}{2})

= 2

\sqrt{{(sin \frac{1}{2} α + cos \frac{1}{2} α)}^{2}}

= 2

\sqrt{1 + sin α}

= 2

\sqrt{1 + k}

Question 10. If

∣ ∣ ∣ a s i n^{2} θ + b s i n θ c o s θ + c c o s^{2} θ - \frac{1}{2} (a + c) ∣ ∣ ∣ \leq \frac{1}{2} k,

then

k^{2}

is equal to

b2+(a−c)2
a2+(b−c)2
c2+(a−b)2
None of these

Discuss Question

Answer: Option A. -> b2+(a−c)2
:
A
(a)

a s i n^{2} θ + b s i n θ c o s θ + c c o s^{2} θ - \frac{1}{2} (a + c)

\frac{1}{2} [- a c o s 2 θ + b s i n 2 θ + c c o s 2 θ]

\frac{1}{2} [b s i n 2 θ - (a - c) c o s 2 θ]

∵ | b s i n 2 θ - (a - c) c o s 2 θ | \leq \sqrt{b^{2} + (a - c)^{2}}

∴ ∣ ∣ ∣ \frac{1}{2} b s i n 2 θ - (a - c) c o s 2 θ ∣ ∣ ∣ \leq \frac{1}{2} \sqrt{b^{2} + (a - c)^{2}}

∴ K = \sqrt{b^{2} + (a - c)^{2}}

Latest Videos

Chapter 1 - GLOBAL STEEL SCENARIO & INDIAN STEEL INDUSTRY Part 1 : (13-04-2024) INDUSTRY AND COMPANY AWARENESS (ICA)

Direction Sense Test Part 1 Reasoning (Hindi)

Chapter 1 - RMHP / OHP / OB & BP Part 1 : (14-02-2024) GPOE

Cube & Cuboid Part 1 Reasoning (Hindi)

Data Interpretation (DI) Basic Concept Reasoning (Hindi)

Counting Figures Part 1 Counting Of Straight Lines Reasoning (Hindi)

Sail E0 free webinar Webinars

Real Numbers Part 7 Class 10 Maths

Real Numbers Part 1 Class 10 Maths

Polynomials Part 1 Class 10 Maths

Latest Test Papers

Pie Chart - Test Paper 1 Data Interpretation Reasoning & DI

Tabulation - Test Paper 2 Data Interpretation Reasoning & DI

Test Paper 1 Direction Sense Test Reasoning & DI

ICA , RDIC,GFM Free Modal Test Paper - Non - Technical Branch Old Syllabus 2022 - SAIL Junior Officer E0

GFM Combined 1 Free Revision Test SAIL JO E-0