MCQs
Heat Radiation, Thermal Properties Of Matter, Dual Nature Of Matter
Total Questions : 247
| Page 1 of 25 pages
Answer: Option D. -> 118 γ2T2Y
:
D
Due to heating the length of the wire increases. ∴Longitudinal strain is produced ⇒ΔLL=a×ΔT
Elastic potential energy per unit volume E=12×Stress×Strain=12×Y×(Strain)2
⇒E=12×Y×(ΔLL)2=12×Y×a2×ΔT2orE=12×Y×(γ3)2×T2=118γ2YT2[Asγ=3aandΔT=T(given)]
:
D
Due to heating the length of the wire increases. ∴Longitudinal strain is produced ⇒ΔLL=a×ΔT
Elastic potential energy per unit volume E=12×Stress×Strain=12×Y×(Strain)2
⇒E=12×Y×(ΔLL)2=12×Y×a2×ΔT2orE=12×Y×(γ3)2×T2=118γ2YT2[Asγ=3aandΔT=T(given)]
Answer: Option B. -> False
:
B
No! You cannot use the thermometer to verify the linear expansion of mercury. This is because the temperature scale itself is defined by making equal markings between 00 C and 1000 C, assuming that mercury expands linearly.
In fact, scientists have now established using statistical physics and other concepts that mercury does not expand exactly in a linear fashion.
Before all this, the only way to guess if a thermometer fluid is a good choice (i.e, expands linearly) was to observe which of them gave consistent results.
:
B
No! You cannot use the thermometer to verify the linear expansion of mercury. This is because the temperature scale itself is defined by making equal markings between 00 C and 1000 C, assuming that mercury expands linearly.
In fact, scientists have now established using statistical physics and other concepts that mercury does not expand exactly in a linear fashion.
Before all this, the only way to guess if a thermometer fluid is a good choice (i.e, expands linearly) was to observe which of them gave consistent results.
Answer: Option C. -> May be in thermal equilibrium
:
C
Let the temperatures of X, Y and Z be Tx, Ty and Tz, respectively.
Now,
Tx ≠ Ty,
and
Tx ≠ Tz.
This does not tell us anything about Ty and Tz, except that they are not equal to Tx.
So, Ty = Tz, and Ty ≠ Tz, both are possibilities!
Hence, option (c) is correct.
:
C
Let the temperatures of X, Y and Z be Tx, Ty and Tz, respectively.
Now,
Tx ≠ Ty,
and
Tx ≠ Tz.
This does not tell us anything about Ty and Tz, except that they are not equal to Tx.
So, Ty = Tz, and Ty ≠ Tz, both are possibilities!
Hence, option (c) is correct.
Answer: Option C. -> 2.28 eV
:
C
The work function is a characteristic of the metal surface - meaning, it does not depend on external factors, like temperature, external electric fields, etc. But in this example, since the electric field is already providing some energy to the electrons, won't the minimum energy needed to come out of the surface decrease now? Yes, true. Then where are we going wrong? Consider the following analogy.
I am really late for class and I am not even within the school. So I decide to climb the boundary wall closest to my class and make a run .
.
To my disappointment, I find the wall to be 3 meters tall, while I stand at 1.5 meters only, and weigh 50 kgs. Since my potential energy on top of the wall would be approximately 50×10×3J=1500J(simple application of P.E = mgh), I would require 1500 J to get on top. I decide to pile a few bricks to a height of 1 meter and stand on top of the pile. Since I'm closer to the top, I will require only (50×10×2) J = 1000 J of energy to make it. Sure, it's easier for me to make the jump now, but - has the height of the wall changed because of the pile of bricks? NO. The wall is still 3 meters high. The pile of bricks is merely an aid (I still had to spend 500 J to get on top of the pile of bricks).
The work function is defined as the minimum energy an electron requires to overcome the binding potential in the absence of external help, like energy from a light source, external electric fields, thermal energy, etc. This is a characteristic feature of the metal surface and does not change, just like the 1500 J of energy required to climb the entire height of the wall in our analogy.
:
C
The work function is a characteristic of the metal surface - meaning, it does not depend on external factors, like temperature, external electric fields, etc. But in this example, since the electric field is already providing some energy to the electrons, won't the minimum energy needed to come out of the surface decrease now? Yes, true. Then where are we going wrong? Consider the following analogy.
I am really late for class and I am not even within the school. So I decide to climb the boundary wall closest to my class and make a run
 .
.To my disappointment, I find the wall to be 3 meters tall, while I stand at 1.5 meters only, and weigh 50 kgs. Since my potential energy on top of the wall would be approximately 50×10×3J=1500J(simple application of P.E = mgh), I would require 1500 J to get on top. I decide to pile a few bricks to a height of 1 meter and stand on top of the pile. Since I'm closer to the top, I will require only (50×10×2) J = 1000 J of energy to make it. Sure, it's easier for me to make the jump now, but - has the height of the wall changed because of the pile of bricks? NO. The wall is still 3 meters high. The pile of bricks is merely an aid (I still had to spend 500 J to get on top of the pile of bricks).
The work function is defined as the minimum energy an electron requires to overcome the binding potential in the absence of external help, like energy from a light source, external electric fields, thermal energy, etc. This is a characteristic feature of the metal surface and does not change, just like the 1500 J of energy required to climb the entire height of the wall in our analogy.
Answer: Option A. -> λ2
:
A
12mV2=32kT
⇒mV=√3mKT
λ=hp=hmV=h√3mKT
⇒λα=1√T
⇒λ1λ2=√T2T1=√273+927273+27=2
⇒λ2=λ12=λ2.
:
A
12mV2=32kT
⇒mV=√3mKT
λ=hp=hmV=h√3mKT
⇒λα=1√T
⇒λ1λ2=√T2T1=√273+927273+27=2
⇒λ2=λ12=λ2.
Answer: Option C. -> 1.0
:
C
By law of conservation of momentum
0=m1→v1+m2→v2⇒m1→v1=−m2→v2
- ve sign indicates that both he particles are moving in opposite direction. Now de-Broglie wavelengths
λ1=hm1v1 and λ2=hm2v2 ; ∴λ1λ2=m2v2m1v1=1
:
C
By law of conservation of momentum
0=m1→v1+m2→v2⇒m1→v1=−m2→v2
- ve sign indicates that both he particles are moving in opposite direction. Now de-Broglie wavelengths
λ1=hm1v1 and λ2=hm2v2 ; ∴λ1λ2=m2v2m1v1=1
Answer: Option B. -> Infinite Line source
:
B
A point source radiates energy equally in all direction
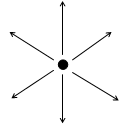
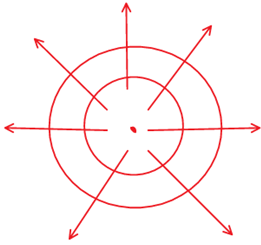
Same is true for a spherical source. Assuming it radiates energy equally in all directions
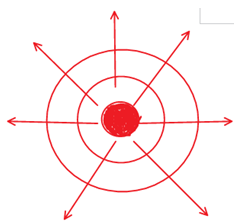
An infinite line source will radiate energy perpendicular to its surface in all direction. So the wave front will be…
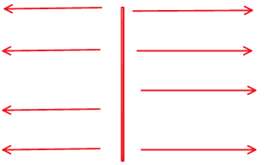
Yup......Right again.
Cylindrical.
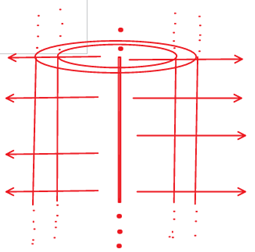
Plane source.
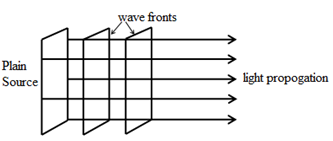
Planar light source will have planar wave fronts.
So correct answer is infinite line source will have a cylindrical wave front.
:
B
A point source radiates energy equally in all direction


Same is true for a spherical source. Assuming it radiates energy equally in all directions

An infinite line source will radiate energy perpendicular to its surface in all direction. So the wave front will be…

Yup......Right again.
Cylindrical.

Plane source.

Planar light source will have planar wave fronts.
So correct answer is infinite line source will have a cylindrical wave front.
Answer: Option B. -> 0.66∘A
:
B
By using λ=hmvrms⇒λ=6.6×10−342×1.67×10−27×3×103=0.66∘A
:
B
By using λ=hmvrms⇒λ=6.6×10−342×1.67×10−27×3×103=0.66∘A
Answer: Option C. -> 1836
:
C
(λeλp)=hmeV×mpVh=mpme=1.67×10−279.1×10−31=1836
:
C
(λeλp)=hmeV×mpVh=mpme=1.67×10−279.1×10−31=1836
Question 10. The resistance of pure platinum increases linearly with temperature (over a small range). We can use this property to measure temperature of different bodies, relative to a scale.
If we scale the thermometer such that a resistance of 80 Ω denotes 0oC and 90 Ω denotes 100oC, what temperature will a resistance of 86 Ω denote?
If we scale the thermometer such that a resistance of 80 Ω denotes 0oC and 90 Ω denotes 100oC, what temperature will a resistance of 86 Ω denote?
Answer: Option C. -> 600C
:
C
A "linear” relation between two quantities, say, Q1and Q2, means the following
Q1=mQ2+c
where mand care constants. This follows from the fact that for a straight line on a plane, yand xare related as,
y=mx+c
m being the slope and c the y-intercept respectively.
In our case, this should be true between the temperatureandthe resistance at that temperature,
Rθ=αθ+β
for some constantsα& β.
Let's find out what these constants are from the information given. We can write
80Ω=α×0oC+β
⇒β=80Ω
90Ω=α×100oC+β
⇒α=90−80100=0.1Ω/oC
Using these values, the temperature(θ)can be written as
86=0.1×θ+80
⇒θ=60oC
:
C
A "linear” relation between two quantities, say, Q1and Q2, means the following
Q1=mQ2+c
where mand care constants. This follows from the fact that for a straight line on a plane, yand xare related as,
y=mx+c
m being the slope and c the y-intercept respectively.
In our case, this should be true between the temperatureandthe resistance at that temperature,
Rθ=αθ+β
for some constantsα& β.
Let's find out what these constants are from the information given. We can write
80Ω=α×0oC+β
⇒β=80Ω
90Ω=α×100oC+β
⇒α=90−80100=0.1Ω/oC
Using these values, the temperature(θ)can be written as
86=0.1×θ+80
⇒θ=60oC
















