Exams > Cat > Quantitaitve Aptitude
GEOMETRY SET II MCQs
Total Questions : 60
| Page 1 of 6 pages
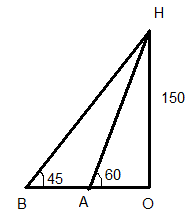
Question 1. Suresh is standing on vertex A of triangle ABC, with AB = 3, BC = 5, and CA = 4. Suresh walks according to the following plan: He moves along the altitude-to-the-hypotenuse until he reaches the hypotenuse. He has now cut the original triangle into two triangles; he now walks along the altitude to the hypotenuse of the larger one. He repeats this process forever. What is the total distance that Suresh walks?
Answer: Option C. -> 12
:
C
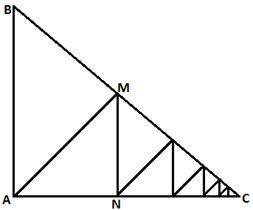
Let M be the end point of the altitude on the hypotenuse. Since, we are dealing with right angle
triangles, ΔMAC ~ΔABC, so AM = 125. Let N be the endpoint he reaches on side AC. Δ
MAC ~Δ NAM, So, MNAM =45. This means that each altitude that he walks gets shorter
by a factor of 45. The total distance is thus an infinite G.P. =[a1−r] = 12
:
C

Let M be the end point of the altitude on the hypotenuse. Since, we are dealing with right angle
triangles, ΔMAC ~ΔABC, so AM = 125. Let N be the endpoint he reaches on side AC. Δ
MAC ~Δ NAM, So, MNAM =45. This means that each altitude that he walks gets shorter
by a factor of 45. The total distance is thus an infinite G.P. =[a1−r] = 12
:
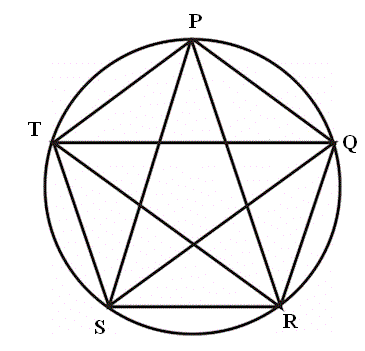
Interior angle = [(2n-4)x90]/n = 108
2x= 360-(108x2) = 144
angle P = 180-144= 36
Total = 36x5= 180
Useful to remember: Sum of angles in a star= 180∘
Shortcut: Clearly the star point trisects the angle in a pentagon. Hence each angle = 108/3 = 36.
Sum of angles = 36*5 = 180
Alternatively: Sum of angles of a n point star = (n – 4) x 180∘, where n = number of sides of a polygon.
Here, n = 5.Sum of angles of a n point star = (5 – 4) x 180∘=180∘.
Answer: Option A. -> (2−√3)√3
:
A
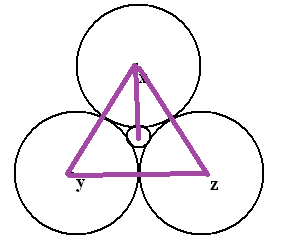
Option (a)
Let the centers of the large balls be x, y, z and radius R.
O is the centre of the smaller ball and radius r...
x, y, z form an equilateral triangle with side equal to 2R.
O is the centroid of this triangle.
Therefore ox=oy=oz=R+r= 23(height of the triangle xyz)
Height=(√32)(2R) =√3R
Therefore R+r = 23(√3R) ⇒ rR = (2−√3)√3
Shortcut:- Using the approximation technique used in class, the radius of the bigger circle: smaller circle is close to 0.2.
:
A

Option (a)
Let the centers of the large balls be x, y, z and radius R.
O is the centre of the smaller ball and radius r...
x, y, z form an equilateral triangle with side equal to 2R.
O is the centroid of this triangle.
Therefore ox=oy=oz=R+r= 23(height of the triangle xyz)
Height=(√32)(2R) =√3R
Therefore R+r = 23(√3R) ⇒ rR = (2−√3)√3
Shortcut:- Using the approximation technique used in class, the radius of the bigger circle: smaller circle is close to 0.2.
Answer: Option D. -> none of these
:
D
Option (d)
AC has to less than 8 as the diameter will be of 8 units. So the correct option is “D” as all are greater than 8
:
D
Option (d)
AC has to less than 8 as the diameter will be of 8 units. So the correct option is “D” as all are greater than 8
Answer: Option C. -> x(x-1)
:
C
Deducing a Pattern:
Taking two circles. The number of points of intersection is 2 at most.
If u consider 3 circles, the number of points of intersection = 6 ( the third circles will have 4 points of intersection with the other 2 circles and those two circles will have 2 points together).
Shortcut:- Assumption & Reverse Gear:
Taking two circles. The number of points of intersection is 2 at most. From this itself, option a, b and d can be eliminated giving answer c.
:
C
Deducing a Pattern:
Taking two circles. The number of points of intersection is 2 at most.
If u consider 3 circles, the number of points of intersection = 6 ( the third circles will have 4 points of intersection with the other 2 circles and those two circles will have 2 points together).
Shortcut:- Assumption & Reverse Gear:
Taking two circles. The number of points of intersection is 2 at most. From this itself, option a, b and d can be eliminated giving answer c.
Answer: Option C. -> 11:54
:
C
Sides are in the ratio 2:4:6
Volume of cuboid= 2x .4x . 6x = 48 x3
Volume of cube= 2.2.2=8
Number of cubes= 6x3
Length of all edges of the cuboid= 144 =4(2x+4x+6x) ⇒ x=3cm
Ratio = 2[72+108+216]6(27) x 6 x 4
= 1154
:
C
Sides are in the ratio 2:4:6
Volume of cuboid= 2x .4x . 6x = 48 x3
Volume of cube= 2.2.2=8
Number of cubes= 6x3
Length of all edges of the cuboid= 144 =4(2x+4x+6x) ⇒ x=3cm
Ratio = 2[72+108+216]6(27) x 6 x 4
= 1154
Answer: Option B. -> 2√3
:
B
Use Eulers triangle theorem which states that the distance,d between the incentre and circumcentre of a trinagle is given by d2 = R(R-2r) where R = circum radius, r= inradius
d2= R(R-2r) = 6(6 - 2 x 2) = 12
d=2√3
:
B
Use Eulers triangle theorem which states that the distance,d between the incentre and circumcentre of a trinagle is given by d2 = R(R-2r) where R = circum radius, r= inradius
d2= R(R-2r) = 6(6 - 2 x 2) = 12
d=2√3
Answer: Option C. -> 2√25+12√3
:
C
option c
let OA and OB be the paths traveled by the two travelers in 2 hours. Let BCâÂ?´ AO at C. then ∠BOC= 180-150= 30∘
In right angled triangle OCB, BC= 62=3 KM and OC= 3√3 km
In right angled triangle ACB, AB2= AC2 + BC2 = (8+3√3)2+32= 100+48√3
AB= 2√25+12√3
Shortcut
√a2+b2−2abcosα; α is the angle between the paths a and b between the 2 people. √100+48is the answer
:
C
option c
let OA and OB be the paths traveled by the two travelers in 2 hours. Let BCâÂ?´ AO at C. then ∠BOC= 180-150= 30∘
In right angled triangle OCB, BC= 62=3 KM and OC= 3√3 km
In right angled triangle ACB, AB2= AC2 + BC2 = (8+3√3)2+32= 100+48√3
AB= 2√25+12√3
Shortcut
√a2+b2−2abcosα; α is the angle between the paths a and b between the 2 people. √100+48is the answer
Answer: Option B. -> Ratio = √946a23√3
:
B
Number of cubes = 2a×3a×9a3×3×3 = 2a3
Diagonal of a cube = √4a2+9a2+81a2
Sum of the diagonals of cubes = 2a3 × 3√3
Ratio =√4a2+9a2+81a22a3×3√3
:
B
Number of cubes = 2a×3a×9a3×3×3 = 2a3
Diagonal of a cube = √4a2+9a2+81a2
Sum of the diagonals of cubes = 2a3 × 3√3
Ratio =√4a2+9a2+81a22a3×3√3