Question
In the given isosceles right angled triangle UVW, a square PQRS is inscribed as shown in the figure. If PV:VS=2:1, what is the ratio of areas of the square to the outer triangle UVW? 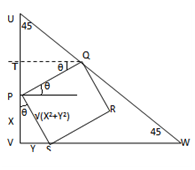
Answer: Option D
:
D
(Area of square / Area of triangle )
= (5(25/2)) = 2:5
Was this answer helpful ?
:
D
Ans: d. 2:5
Using variables
In the given figure, we draw QT || VW.
Δ PTQ and Δ PVS are congruent (A,A,A and side)
Hence PT=Y, QT=X=UT (also since ΔUTQ and ΔUVW are similar).
Thus UV=UW=2X+Y. Area of square: X2+Y2; Area of ΔUVW= 12 *(2X+Y)2.
Given X=2Y, X2+Y2: ( 12 *(2X+Y)2) = 5Y2: ( 25Y2* 12 ); = 25.
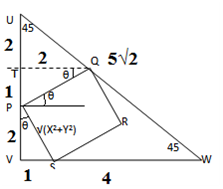
Using numbers,You can solve the problem faster as follows:
PV=2, SV=1 => PS= √5 ⇒ Area of square =5
PTQ congruent to PVS
PT=1 and QT=2
UT=TQ (45-45-90) ⇒ UT= 2
Now UV= 5 ⇒ WV=5 (45-45-90)
UW=5√2
(Area of square / Area of triangle )
= (5(25/2)) = 2:5
Was this answer helpful ?


















Submit Solution