Question
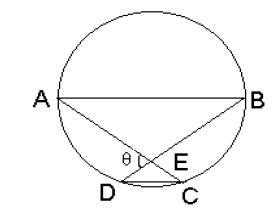
In the given figure AB is a diameter of the circle, CD is a chord parallel to AB, and AC intersects BD at E. If the ratio of area of triangles AEB and DEC= 4: 1, then find out the value of (\theta\)
. 
Answer: Option B
:
B
Was this answer helpful ?
:
B
Join AD. As AB is the diameter ∠ ADB = 90. And hence ΔADB is a right angle triangle.
Triangles AEB and DEC are similar hence if the ratio of area is 4: 1, ratio of sides will be 2:1.
So, AE: DE = 2: 1. In triangle ADE, hypotenuse AE = 2, DE = 1 AD2 = 4 – 1 = 3. AD = √3
So, ∠ AED = 60 ∘ .
Was this answer helpful ?
More Questions on This Topic :
Latest Videos
Latest Test Papers
Submit Solution