In the figure given below ABCD is a square and ΔPDC is isosceles with PD = PC.

Sail E0 Webinar

Question

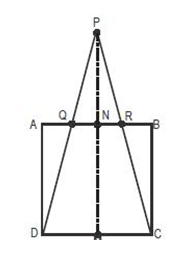
In the figure given below ABCD is a square and ΔPDC is isosceles with PD = PC. If the area of $Δ$ PDC is twice the area of the square, then find the ratio of the area of $Δ$ PDC that lies outside the square to the area of the square.

Options:

A .

\frac{3}{2}

B .

\frac{4}{5}

C .

\frac{9}{8}

D .

\frac{10}{7}

Answer: Option C
:
C

Drop a perpendicular PM on the side DC.
Let PN be 'x' and side of square be 2a
$\Rightarrow$ $\frac{1}{2} \times 2 a \times$ (2a + x) = 8a $^{2}$
$\Rightarrow$ x = 6a
$\frac{Δ P Q R}{Δ P D C} = {(\frac{6 a}{8 a})}^{2} = \frac{9}{16} \Rightarrow Δ P Q R = \frac{9}{16} Δ P D C$
$Δ P Q R = \frac{9}{16} (2 \times A B C D)$
Required Ratio = $\frac{9}{8}$
Hence, option (c)

Was this answer helpful ?

Next Question

Submit Solution

More Questions on This Topic :

Question 1. The infinite sum 513+55132+555133+5555134+..... equals ....

Question 2. The set of all positive integers is the union of 2 disjoint subsets {f(1),f(2),f(3),...}& {g(1),g(2),g(3),...}, wh....f(1)<f(2)<f(3)<.....& g(1)<g(2)<g(3)<...... g(n)=f(f(n))+1 for n = 1,2,3,...... What is the value of g(1)?

Question 3. ax + 2y = 30 and 3x + by = 15 are two equations in variables x and y. For what condition you cannot find the solution ....condition you cannot find the solution of these simultaneous equations.

Question 4. In the figure, AB = OA(radius of the circle). If Y = kX. The value of k is ___.....

Question 5. Three distinct prime numbers less than 10 are taken and all the numbers are formed by arranging all the digits taken. ....more than 13. What is the product of the digits?

Question 6. PQR is a right angled triangle with PQ=8, QR=6, QT as altitude. If a circle is drawn with QT as diameter, what is the ar....as diameter, what is the area of the shaded region?

Question 7. If S1,S2,S3,....Sn are the sums of infinite geometric series whose first terms are 1, 2, 3,...n and whose ratios ....ratios are 12,13,14,1(n+1) respectively, then find the value of S21+S22+S23+....+S26

Question 8. In a country, all numbers are represented with the help of 3 alphabets, a, b & c. 15 is written as abc; 6 is written....as bcbc. How would 17 be written in that country?

Question 9. There are two women participating in a chess tournament. Every participant played two games with the other participant....men played with the women. How many games were played?

Question 10. ABCABC is a six digit number where A,B,C are three consecutive natural numbers. Find the remainder when ABCABC is divi....numbers. Find the remainder when ABCABC is divided by 1001?

Chapter 1 - GLOBAL STEEL SCENARIO & INDIAN STEEL INDUSTRY Part 1 : (13-04-2024) INDUSTRY AND COMPANY AWARENESS (ICA)

Direction Sense Test Part 1 Reasoning (Hindi)

Chapter 1 - RMHP / OHP / OB & BP Part 1 : (14-02-2024) GPOE

Cube & Cuboid Part 1 Reasoning (Hindi)

Data Interpretation (DI) Basic Concept Reasoning (Hindi)

Counting Figures Part 1 Counting Of Straight Lines Reasoning (Hindi)

Sail E0 free webinar Webinars

Real Numbers Part 7 Class 10 Maths

Real Numbers Part 1 Class 10 Maths

Polynomials Part 1 Class 10 Maths

Chapter 3.1 : Overview of Finance & Accounts Department Chapter 3 : Finance & Accounts SAIL E0 - GFM 2024

Chapter 2.1 : Overview Chapter 2 : Materials Management SAIL E0 - GFM 2024

Chapter 1.1 : Personnel Functions- An overview Chapter 1 : Personnel Management SAIL E0 - GFM 2024

GPOE / GPA Combined 1 Free CBT Mock Test SAIL E0 2024

CBT Mixed Test 1 GPOE/GPA SAIL E0 2024