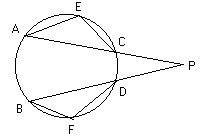
Angle AEC=115. Suppose there is a point X in the major segment of chord AC. AECX will be a cyclic quadrilateral. Therefore , Angle AEC + Angle AXC =180

$\Rightarrow$ Angle AXC= 65

$\Rightarrow$ Angle AOC=130 (Measure of arc AC at the centre O)

Similarly Angle BOD = 100

Therefore, Angle AOB (or measure of arc AB) + Angle COD (or measure of arc CD)= 360 - (100+130) = 130 ---- (1)

Now we know the theorem that if there are two secants PA and PB and P lies outside the circle , then Angle P = $\frac{1}{2}$ ( measure of arc COD - measure of arc AOB) =30 (given in the ques) -- (2)$\Rightarrow$ ( measure of arc CD - measure of arc AB) =60 -- (3)

You can see that equations (1) and (3) are simultaneous equations in measure of arc AB and measure of arc CD .So, finally measure of arc AB is $\frac{(130+60)}{2}$ = 95.