Question
ABCD is a cyclic quadrilateral while triangle ABF and triangle CEF are similar triangles. Which of the following cannot be the value of angle BAC if ∠BEC = 30∘?
 
Answer: Option A
:
A
Let ∠ACD = ∠BAC = x. Connect D to B such that the line intersects AC at O.
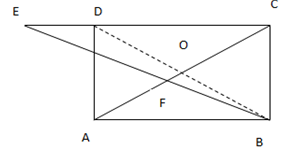
As the quadrilateral ABCD is cyclic, ∠AOD = 2 * ∠ACD. (Because O is the centre of the circle around the cyclic quadrilateral, and angle subtended at center is twice the angle subtended at a point on the circumference by the same arc AD, here.
So, ∠AOD = 2x
∠EBA = ∠BED = 30
∠BDC = ∠DBE + 30
∠AOD is exterior angle for triangle COD.
So, ∠AOD = 2x = 30 + ∠DBE + x
∠x = 30 + ∠DBE.
Was this answer helpful ?
:
A
Let ∠ACD = ∠BAC = x. Connect D to B such that the line intersects AC at O.
As the quadrilateral ABCD is cyclic, ∠AOD = 2 * ∠ACD. (Because O is the centre of the circle around the cyclic quadrilateral, and angle subtended at center is twice the angle subtended at a point on the circumference by the same arc AD, here.
So, ∠AOD = 2x
∠EBA = ∠BED = 30
∠BDC = ∠DBE + 30
∠AOD is exterior angle for triangle COD.
So, ∠AOD = 2x = 30 + ∠DBE + x
∠x = 30 + ∠DBE.
 So, ∠BAC can't be less than 30 degrees so 'a' is the answer.
Â
Was this answer helpful ?
More Questions on This Topic :
Latest Videos
Latest Test Papers
Submit Solution