Question
Solve the following system of equations:
8v−3u=5uv
6v−5u=−2uv
Â
Answer: Option B
:
B
Divide the given equations by uv,
8v−3u=5uv⇒8u−3v=5...(1)
6v−5u=−2uv⇒6u−5v=−2...(2)
Assume 1u=x and 1v=y
Put the values of 1u and 1v in (1) and (2)
8x−3y=5...(3)
6x−5y=−2...(4)
Solving equations (3) and (4) we get x and y
Multiply (3) with 5 and (4) with 3 to equate the coefficients of y.
40x−15y=25
18x−15y=−6
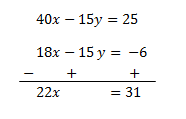
⇒x=3122⇒u=2231
Substituting x in (3)
8×3122−3y=5→3y=6911
Â
→y=2311⇒v=1123
So, u=2231 and v=1123
Was this answer helpful ?
:
B
Divide the given equations by uv,
8v−3u=5uv⇒8u−3v=5...(1)
6v−5u=−2uv⇒6u−5v=−2...(2)
Assume 1u=x and 1v=y
Put the values of 1u and 1v in (1) and (2)
8x−3y=5...(3)
6x−5y=−2...(4)
Solving equations (3) and (4) we get x and y
Multiply (3) with 5 and (4) with 3 to equate the coefficients of y.
40x−15y=25
18x−15y=−6
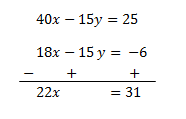
⇒x=3122⇒u=2231
Substituting x in (3)
8×3122−3y=5→3y=6911
Â
→y=2311⇒v=1123
So, u=2231 and v=1123
Was this answer helpful ?
More Questions on This Topic :
Latest Videos
Latest Test Papers
Submit Solution