Which of the following numbers cannot be determined from the information given?
Options:
A.Number of labour experts from the Americas.
B.Number of health experts from Europe.
C.Number of health experts from Australasia.
D.Number of experts in refugee relocation from Africa.
Answer: Option D
: D

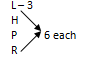
(i) As the labour expert is half of each of the other, so the only possible combination is (ii) Statement (d): If the number of Australasia expert is 1 less, i.e. total experts are 20 American experts will be twice as each of other. The only combined possible is Americas 8. Australasia 4 + 1 = 5 Europe 4 Africa 4 Now, we need to workout the various options possible in the blank cells. AfricaAmericaAustraliaEuropeTotalLabour01113Health22116PS12216RefugeeAllocation13116Total485421

AfricaAmericaAustraliaEuropeTotalLabour01113Health13116PS12216RefugeeAllocation22116Total485421

AfricaAmericaAustraliaEuropeTotalLabour01113Health13116PS21216RefugeeAllocation13116Total485421

Previous Next

Submit Solution

Your email address will not be published. Required fields are marked *

More Questions on This Topic :

Question 1. If Mr. Shyam pays the workers Rs. 3040 in all for this job, how many workers work on day 3?
  1.    3
  2.    2
  3.    4
  4.    Cannot be determined
Answer: Option A
: A

The man-hours required for the job =(304020)=152. The Total number of workers who worked on this job for 6 days =(1528)=19. We get the following possibilities for the number of workers: Day1Day2Day3Day4Day5Day6323434343234
Question 2. What should be the new tax percentage on Brand 2 so that the tax collected by value for Brand 1 and 2 are the same?
  1.    12%
  2.    16.3%
  3.    20.25%
  4.    24.56%
Answer: Option B
: B

New value of tax collected by brand 2 =9135000. Hence new percent value of tax should be 913500056000000×100=16.3125%.
Question 3. Rob, an American expert in refugee relocation, was the first keynote speaker in the conference. What can be inferred about the number of American experts in refugee relocation in the conference, excluding Rob?

i. At least one

ii. At most two
  1.    Only i and not ii
  2.    Only ii and not I
  3.    Both i and ii
  4.    Neither i nor ii
Answer: Option C
: C

AfricaAmericaAustraliaEuropeTotalLabour01113Health22116PS12216RefugeeAllocation13116Total485421

AfricaAmericaAustraliaEuropeTotalLabour01113Health13116PS12216RefugeeAllocation22116Total485421

AfricaAmericaAustraliaEuropeTotalLabour01113Health13116PS21216RefugeeAllocation13116Total485421
Question 4. What is the minimum number of workers required to finish the job in one day?___

: For the minimum number of workers to complete the job in one day, the job must have been completed in the minimum possible number of man-hours in 6 days.
This is possible if the number of workers working on Day 1,2,3,4,5, and 6 are 3,2,1,2,3 and 4 respectively. Thus, the minimum number of man-hours required for the job =(3+2+1+2+3+4)×8=120.
The minimum number of workers required to complete the job in one day =(1208)=15.
Question 5. In the league tournament with the conditions as described in the first question, a bookie Charlie follows the following system. In a match between two teams "a” and "b”, the team "a” wins more of their previous matches. If team "a” wins this match, he will pay Rs. 1.5 for every Re. 1 bet on team "a”. If team "b” wins this match, he will pay Rs. 2 for every Re. 1 bet on team "b”. In every match, equal money was bet on both the teams playing in that match. What was Charlie's gain, as a fraction, on the total money that he bet?
  1.    −14
  2.    0
  3.    14
  4.    12
Answer: Option C
: C

Based on the information in the previous question, Charlie gets, say Rs 1 each from the betters of the two teams. In 6 matches, Charlie gets Rs 12. We know that the better team is winning in each case; hence his net gain is 50 paise in 6 matches ⇒ his total gain =(0.5×6)12=14
Question 6. If one of the pairs is given, then what is the probability that all the other required pairs can be determined?
  1.    410
  2.    510
  3.    710
  4.    310
Answer: Option B
: B

The correct option is (b). If the pairs (BLUE, GREEN), (BLUE, PINK), (BLUE, PURPLE), (RED, PURPLE) and (YELLOW, PURPLE) are given, then all other pairs can be determined, while if the pairs (BLUE, YELLOW), (RED, YELLOW), (RED, PINK), (GREEN, PINK) and (GREEN, PURPLE) are given, then all other pairs cannot be determined. Therefore, required probability. =Totalnumberoffavourablecasestotalnumberofpossiblecases=510